Jackknife Procedure
To calculate an estimate of the standard error of θ-hat which is an estimate of some parameter θ, we can use a nonparametric procedure called the Jackknife method. This uses the following procedure:
- For each element xi in the sample (actually the pair (xi, yi) for Deming regression), calculate θi-hat in the same way as θ-hat was calculated except that the element xi is left out of the calculation.
- Calculate
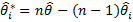
- Calculate the mean of these values, called the jackknifed estimate by using the following formula

- The jackknifed estimate of the variance and standard error of is now given by the formulas
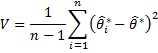
It is easy to see that the jackknifed estimate of the variance can also be calculated more simply as n – 1 times the deviation squared of the θi-hat values. Thus
We can use this technique to find confidence intervals for the regression coefficients b0 and b1 based on the t distribution with n–1 degrees of freedom. We can also calculate a confidence interval for the prediction of y for a given value of x in the same manner.
Examples
Example 1: Calculate the standard error for coefficients from Example 1 of Deming Regression Basic Concepts.
First, we define x̄i, ȳi, ui, vi, ri to be the same as x̄, ȳ, u, v, r from Property 1 of Deming Regression Basic Concepts except that the sample pair (xi, yi) is omitted.
and so the sum of squared data elements excluding xi is equal to u + nx̄2 – xi2, from which it follows that
and so the sum product of data elements excluding xi and yi is equal to r + nx̄ȳ – xiyi, from which it follows that
Using the formulas
Using these formulas, we can calculate the standard errors of the intercept and slope for Example 1 of Deming Regression Basic Concepts as shown in Figure 1.
Figure 1 – Standard errors of coefficients
Here, the values for x̄, ȳ, u, v, r are shown in range E14:I14, and can be calculated exactly as shown in Figure 1 of Deming Regression Basic Concepts.
Cell E4 contains the formula =($A$13*E$14-B4)/($A$13-1). Note that it could also be calculated by the array formula
=AVERAGE(IF($A$4:$A$13=$A4,””,B$4:B$13))
Similarly, cell F4 contains the formula =($A$13*F$14-C4)/($A$13-1).
Cell G4 can be calculated by the formula
=G$14-$A$13*(E$14-B4)^2/($A$13-1)
or optionally by the array formula
=SUMSQ(IF(A$4:A$13=A4,””,B$4:B$13-E4))
Similarly, cell H4 can be calculated by the formula
=H$14-$A$13*(F$14-C4)^2/($A$13-1)
Cell I4 can be calculated by the formula =I$14-$A$13*(E$14-B4)*(F$14-C4)/($A$13-1) or optionally by the array formula =SUM(IF(B$4:B$13=B4,””,(B$4:B$13-E4)*(C$4:C$13-F4))).
Now we apply the jackknifing procedure. Cell J4 contains the formula =F4-K4*E4 and cell K4 contains the formula =($B$15*H4-G4+SQRT(($B$15*H4-G4)^2+4*$B$15*I4^2))/ (2*$B$15*I4). Finally, cells J16 and K16 contain =DEVSQ(J4:J13)*($A$13-1) and =DEVSQ(K4:K13)*($A$13-1). Cells J17 and L17 contain =SQRT(J16/$A$13) and =SQRT(K16/$A$13), yielding the standard error for the intercept of 1.3375 and for the slope of 0.2193.
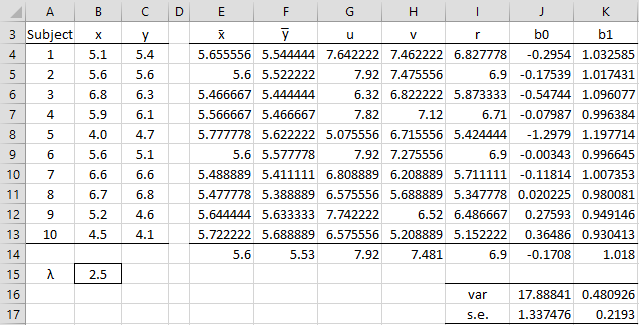
The usual regression coefficient table can now be calculated as shown in Figure 2.
Figure 2 – Regression coefficient table
Note that we use df = n–2 = 10–2 = 8, although some implementations use df = n–1 = 9.
We see from Figure 2 that the slope coefficient is significant.
Observation: When the parameter θ is a smooth function, the delete-1 jackknifing approach described above does a pretty good job in computing the standard error, but when θ is not smooth (i.e. a small change in the sample can result in a large change in the estimate of θ), then this approach doesn’t work very well. An example of such a θ is the median. For such θ, delete-d jackknifing or bootstrapping work better.
Delete-d jackknifing approach
- For each subset T with d elements from the sample, calculate θT-hat in the same way as θ-hat was calculated except that the elements in T are left out of the calculation.
- Calculate the mean of the θT-hat, labeled θ-tilde, using the following formula where n = the sample size

- The jackknifed estimate of the standard error of θ is now given by the formula
Note that some would replace n – d by n in the above formula.
In practice, it is best to choose a value of d between the square root of n and n.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Reference
NCSS (2016) Deming regression
https://www.ncss.com/wp-content/themes/ncss/pdf/Procedures/NCSS/Deming_Regression.pdf
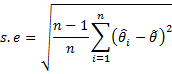
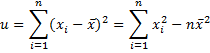

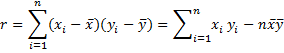

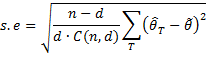
Hi, the formula you wrote for the V calculation in J16 is =DEVSQ(J4:J13)*($A$13-1), but, according to the formula you reporte in the upper part of the text (after point 4) it should have been =DEVSQ(J4:J13)/($A$13-1). This difference is not clear to me
Hi Maurizio,
I have just checked the results obtained by Real Statistics against those obtained by R on the same data and the variance and standard errors agree.
It does seem that the formula should use “/” instead of “*”, but apparently this is not the case. I still need to track down why.
Charles
Hi, I checked also NCSS and infact they agree, because the SE formula you reported have SQR((n-1)/n…) that is the same used in R and is the resulting from your excel.
The discrepancy is in text formulas in italic:
V has 1/n-1
SE has V/n
So SE should have 1/((n-1)*n) instead has n/n-1 that seems the correct one
Hello Maurizio,
Sorry for the delayed response.
I am a bit confused about your email. You state that SE should use 1/((n-1)*n) instead has n/(n-1). But you also state that R uses SQR((n-1)/n…), but doesn’t this contradict your previous statement?
Charles
Thank you very much for the materials. I have a question. The value of lamda is 2.5 in the table. How it has come? Please help me.
Regards,
Tapas.
Hello Tapas,
The example comes from the following webpage
https://www.real-statistics.com/regression/deming-regression/deming-regression-basic-concepts/
This webpage shows how to calculate the value of lambda.
Charles
How to use jackknife method for empirical bayes beta binomial model?
I am sorry, but I have not included this topic as yet on the Real Statistics website. I expect to be adding Baysian statistics topics in the future.
Charles
how does one calculate the standard error at a percentile?
Sorry, but I don’t understand your question.
Charles
Hi Charles. I perfumed Deming regression on my data but need to calculate the 95% confidence interval for the 25th percentile. How do can I do this?
By the way, your website has been a great help to me. Thanks
Hi Craig,
I am pleased that the website has been helpful.
The 25th percentile refers to what statistic? (the slope and/or intercept?)
This example is very useful and informative. However, when I compute the variance and SE of the jackknifed estimates (col j & k), I obtain very different values from those in the table.
var(b0) = .2208
se(b0) = .1486
var(b1) = .005938
se(b1) = .02437
Shouldn’t cells j16 and k16 be divided by 9, not multiplied by 9?
Thank you.
Hi Tim,
These cells should be multiplied by 9 as shown in step 2 of the webpage.
I have checked the results with those generated by the NCSS software package and they agree.
Charles
Appreciate this technique very much – crystal clear down to MS Excel!
This website has been a life saver for me. I’ve been tasked with trying to replicate the results of a Deming Regression performed by a commercial product in excel and thanks to this website I have successfully calculated the slope and intercept. Is there another method (besides jack knifing) for determine the standard error of the slope and intercept. When I use the jack knife procedure as described i get the same 95% CI as the excel addon “Analyse-it” but the 95% CI from the commercial statistical software i’m using is much wider for the intercept (it is similar for the slope). I tried reading digging into the software documentation to see if they give information on how the CI is calculated but so far no luck.
Any guidance that anyone has would be greatly appreciated!
Sherri,
Bootstrapping is another approach for creating confidence intervals.
Charles