Basic Concepts
In the rest of this part of the website, we have presented various analytic solutions to queueing problems. We now show how to create a simulation.
We demonstrate two simulations. The first is a queueing system with one server and the second contains multiple servers. In fact, we will show two types of simulations for the first case: simulation by customer and simulation by events. We could have done the same for the multi-server case.
In our examples, we will use queueing systems with exponential arrival and service rates, but the actual simulation can be used with any arrival and service rates.
Topics
- Single-server model (by customer) – this webpage
- Single-sever model (by events)
- Multi-server model
Single Server Example
Example 1: Model an M/M/1 queueing system where λ = 5 and μ = 6 using simulation.
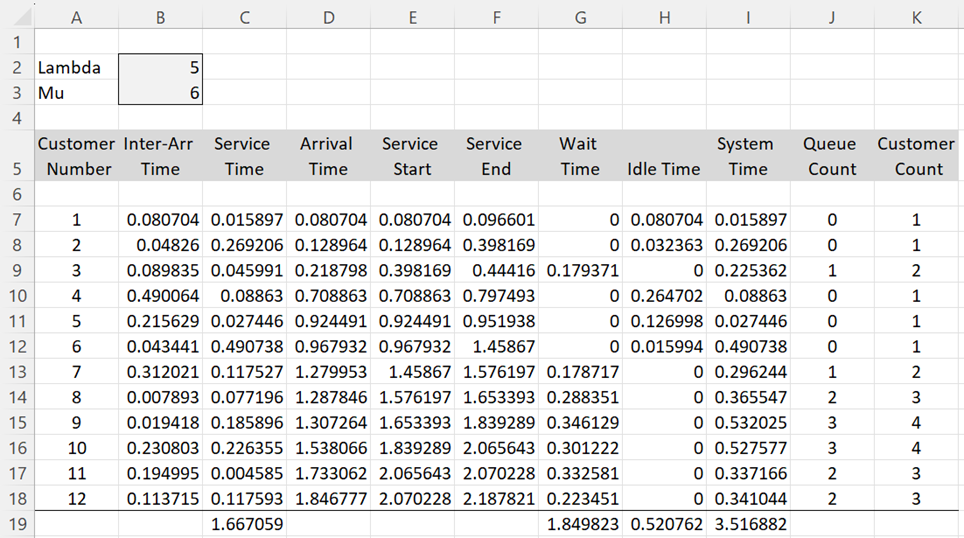
We show the results for the first 12 customers in the system in Figure 1.
Figure 1 – M/M/1 simulation
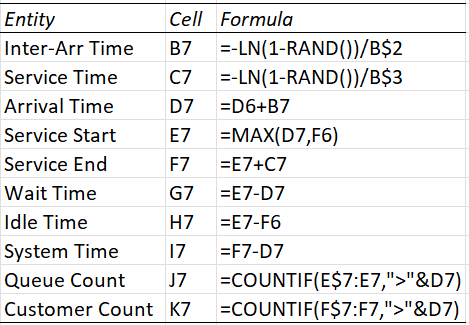
The formulas used in row 7 of Figure 1 are shown in Figure 2. The other formulas are obtained by highlighting range B7:K18, and pressing Ctrl-D. Note that the customer counts in columns J and K are at the time of the latest arrival (column D) for each row. Some column counts are shown in row 19.
Figure 2 – Formulas used in Figure 1
Note that inter-arrival and service times in cell B7 and C7 (and other entries in columns B and C) can also be calculated by the Real Statistics formulas =EXPON_INV(RAND(),B$2) and =EXPON_INV(RAND(),B$3). The formulas shown in Figure 2 are equivalent. Since RAND() and 1-RAND() are both random numbers between 0 and 1, we could also use the formula =-LN(RAND())/B$2 in cell B7.
Note too that the system time in cell I7 can also be calculated by the formula =C7+G7, and similarly for the other values in column I. Finally, note that the value in cell J7 can be calculated by =MAX(0,K7-1), and similarly for the other values in column J.
Simulation Results
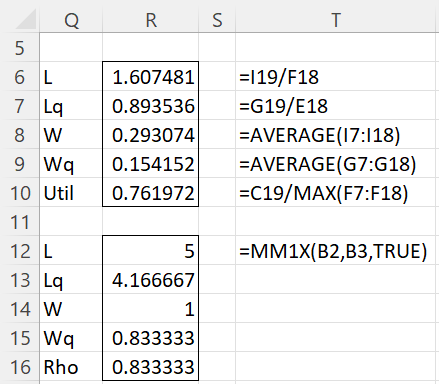
From the data in Figure 1, we arrive at the values in Figure 3.
Figure 3 – L, Lq, W, Wq, ρ values
The top part of the figure is based on the simulation data. The values in the bottom part of the figure are calculated using analytic queueing theory formulas. As you can see the values are quite different.
There are several reasons for this. First, to obtain credible results from the simulation, we need to let the simulation run for a much longer period of time. 12 customers are too few. Second, the analytic formulas are based on the steady-state situation. It is unlikely that the simulation yet entered a steady state.
Note too that the simulation shown above is valid even for single server queueing models where the arrival and/or service rates are not exponentially distributed (i.e. G/G/1 models) provided you can provide the values in columns B and C.
Worksheet Function
Real Statistics Function: The Real Statistics Resource Pack provides the following worksheet function where R1 is an array containing customer inter-arrival times and R2 is an array containing the corresponding service times.
QUEUE_SIM(R1, R2, lab): returns an array with the values L, Lq, W, Wq, and Rho based on a simulation of a queueing model for m customers with inter-arrivals and service times of m customers in R1 and R2. If lab = TRUE (default FALSE) then a column of labels is appended to the output.
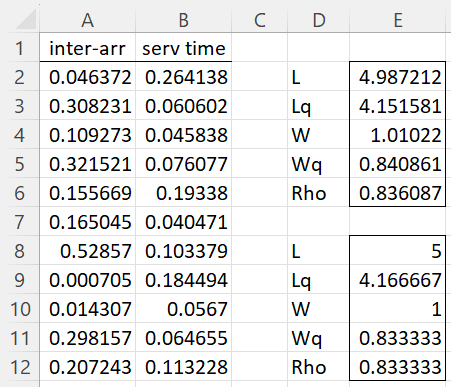
For Example 1, we enter the formula =-LN(RAND())/5 in cell A2 and =-LN(RAND())/6 in cell B2. We next highlight the range A2:B10001, and press Ctrl-D. Next, we enter the array formula =QUEUE_SIM(A2:A10001,B2:B10001,TRUE) in range D2:E6.
The results of the simulation for 10,000 customers are shown in Figure 4. We assume that the number of iterations before a steady state is reached is small so that we can ignore these in calculating our results. The output from =MM1X(5,6,TRUE) is shown in range D8:E12. We observe that values from the simulation are pretty close to the analytic values.
The simulation is especially useful for G/G/1 models where we don’t have an analytic alternative.
Figure 4 – Larger simulation
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Reference
Leong, T-Y. (2007) Simpler spreadsheet simulation of multi-server queues. INFORMS Transactions on Education 7(2):172-177.
https://ink.library.smu.edu.sg/sis_research/215/