Basic Concepts
This model is like an M/M/1 queueing model with pre-emptive priority queueing, except that multiple servers are possible.
Alternatively, we can view this model like an M/M/s queueing model, except that there are multiple priority classes. The lowest priority customer being served is pre-empted when a higher priority customer arrives. This new arrival replaces this customer in the server and the lower-priority customer returns to the front of the queue to be served when a server is free unless a higher priority customer is in the queue. If two or more lowest priority customers are available for pre-emption, it doesn’t matter which one is bumped.
Example
Example 1: Suppose a hospital emergency room deals with three classes of patients: critical, serious, and stable. These are listed in priority order, with critical being the highest priority. Patients arrive based on an exponential distribution with mean arrival rates of .2, .6, and 1.2 per hour for the three classes respectively. Each medical team can treat 3 patients per hour irrespective of the priority level. We use an M/M/s model with pre-emptive priorities.
Determine queueing time per patient in each priority class based on 1 or 2 medical teams (i.e. s = 1 or 2).
This example is taken from the Hillier and Lieberman book listed below in the references.
One Server
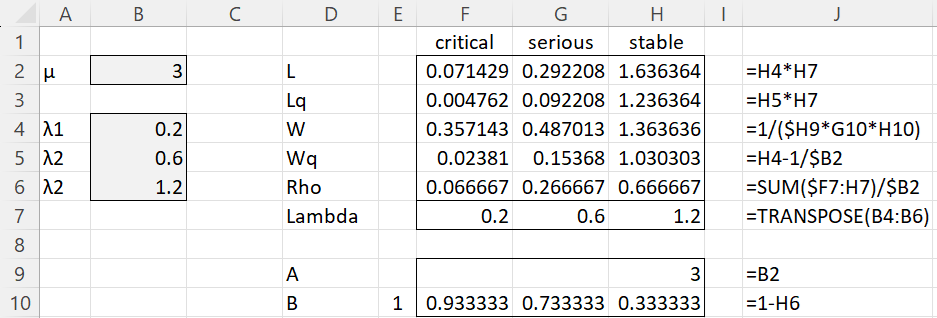
For one medical team, we have the results shown in Figure 1 using the approach shown in M/M/1 (i.e. s = 1) with preemptive priority queueing or Real Statistics’ MM1PP function.
Figure 1 – Pre-emptive priority M/M/1 model
We can obtain the results shown in range F2:H6 by using the array formula MM1PP(B4:B6,B2). Actually, for the purpose of this example, we only need the Wq results.
Two servers
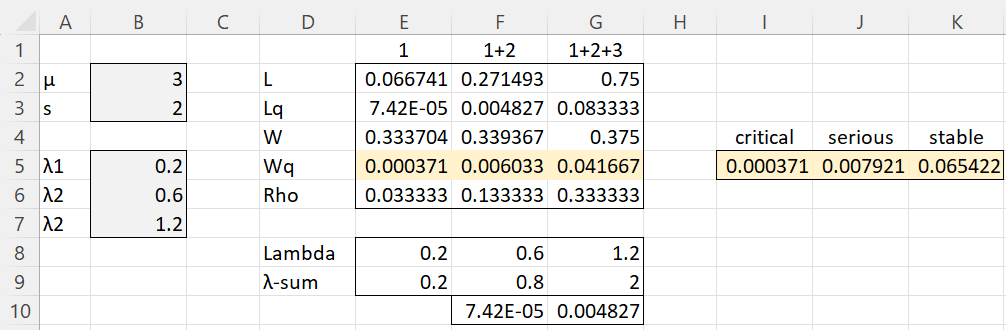
When there are 2 servers, we first obtain the results from three M/M/s queueing models with s = 2 and μ = 3, as shown in Figure 2. For the first of these models, we use λ = λ1. For the second we use λ = λ1+λ2, and for the third λ = λ1+λ2+λ3. We create these three models by placing the array formula =TRANSPOSE(B5:B7) in E8:G8. Then we insert the formula =E8 in cell E9, =E9+F8 in cell F9, highlight F9:G9, and press Ctrl-R. We next place the array formula =MMs(E9,$B2,$B3) in E2:E6, highlight E2:G6 and press Ctrl-R.
Figure 2 – M/M/s models with s = 2
Calculations
We now only look at the Wq values. For the critical class, Wq = .000371 (shown in cell E5). The situation is a little more complicated for the other two classes. For the serious class, we use the Wq shown in cell F5, but first, we need to disaggregate the critical and serious components of the value in F5. This is done by noting that
We know all the components of this equation with the exception of Wq2. Solving for Wq2, we obtain
To find Wq for stable patients (priority 3), we need to disaggregate them from the value in cell G5. This is done using the following equation
As before, solving for Wq3, we obtain
We can do the same in Excel, as shown in Figure 1, by placing the formula =SUMPRODUCT($E8:E8,$I5:I5) in cell F10, highlighting =F10:G10, and pressing Ctrl-R. Finally, we place the formula =E5 in cell I5 and =(F9*F5-F10)/F8 in cell J5, highlight J5:K5, and press Ctrl-R.
Worksheet Function
Excel Function: The Real Statistics Resource Pack supports the following array function for an M/M/s model with pre-emptive priority queueing where R1 is a column or row array with the arrival rates for m priority classes in priority order from highest to lowest.
MMsPP(R1, μ, s): returns a row array with Wq for the m priority classes
Thus, we can obtain the values in range I5:K5 in Figure 2 via the array formula =MMsPP(B5:B7,B2,B3).
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Ross, S. M. (2014) Introduction to probability models, 11th Ed. Academic Press
https://ebin.pub/introduction-to-probability-models-11nbsped-0124079482-9780124079489.html
Sztrik, J. (2021) Basic queueing theory
https://irh.inf.unideb.hu/~jsztrik/education/16/SOR_Main_Angol.pdf
Shores, T. S. (2017) Queueing theory basics and models
No longer available online
Hillier, F. S., Lieberman, G. J. (2010) Introduction to operations research. 9th Ed.