M/M/1 with non-preemptive priority queueing and variable service means

Basic Concepts

We now consider the M/M/1 model with non-preemptive priority queueing, except that now the service rates for the priority classes can vary. The mean service rate for the kth priority class is μk (and the arrival rate is λk).

Properties

We suppose that we have m priority classes where class 1 is of higher priority than class 2, etc. Using the notation from Queueing Theory, for k = 1, 2, …, m, the mean queueing time for customers from priority class k is

Wq for class k

where

A_k

B_k

As usual, the mean time that customers from priority class k remain in the system is

W_k

By Little’s Law

Lk and Lqk

The above formulas hold when the system reaches a steady state, which is applicable when

Example

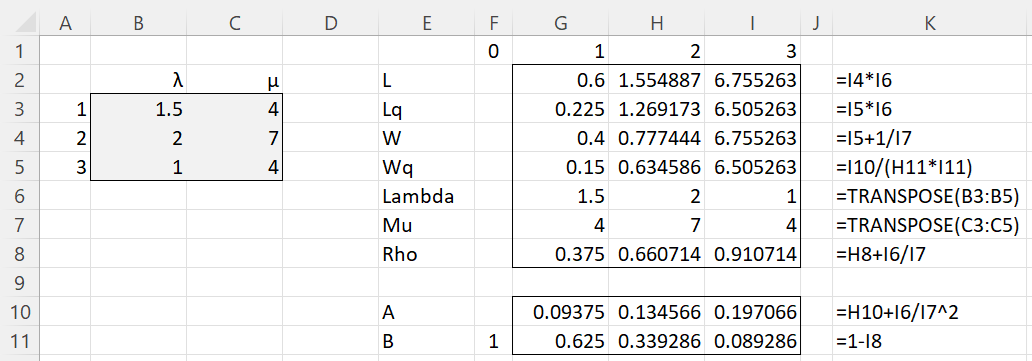
Example 1: Calculate L, Lq, W, and Wq for the M/M/1 queueing model with three priority classes where the arrival rates and the service rate are as described in columns B and C of Figure 1.

The results are shown on the right side of Figure 1. Column K displays the formulas in column I.

M/M/1 non-preemptive priority model

Figure 1 – M/M/1 with non-preemptive priority queueing

Worksheet Functions

Excel Functions: The Real Statistics Resource Pack supports the following array function. Here, R1 is a row or column array or cell range that contains the arrival rates for the various priority classes. R2 is a row or column array or cell range that contains the service rates for the various priority classes. 

MM1PS(R1, R2, lab): returns an array with L, Lq, W, Wq, ρ for each priority class in an M/M/1 non-preemptive priority queueing model.

If lab = TRUE (default FALSE) then an extra column of labels is appended to the output.

You can obtain the values in Figure 1 via the array formula

=MM1PS(B3:B5,C3:C5,TRUE)

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Ross, S. M. (2014) Introduction to probability models, 11th Ed. Academic Press
https://ebin.pub/introduction-to-probability-models-11nbsped-0124079482-9780124079489.html

Sztrik, J. (2021) Basic queueing theory
https://irh.inf.unideb.hu/~jsztrik/education/16/SOR_Main_Angol.pdf

Shores, T. S. (2017) Queueing theory basics and models
No longer available online

Hillier, F. S., Lieberman, G. J. (2010) Introduction to operations research. 9th Ed.
http://www.maths.lse.ac.uk/Personal/stengel/HillierLieberman9thEdition.pdf

Leave a Comment