Basic Concepts
This model is like the M/M/1 with non-preemptive priority queueing, except that now there can be multiple servers. As in this model, we define the total arrival rate as λ = λ1 + λ2 + … + λm. As for the M/M/s queueing model, we define τ = λ/μ and ρ = τ/s where s = the number of servers. A steady state is achieved when ρ < 1.
Properties
Now L, Lq, W, and Wq are defined as for the M/M/1 model with non-preemptive priority queueing except that
Note that when s = 1 these formulas as equivalent to those for the M/M/1 case.
Example
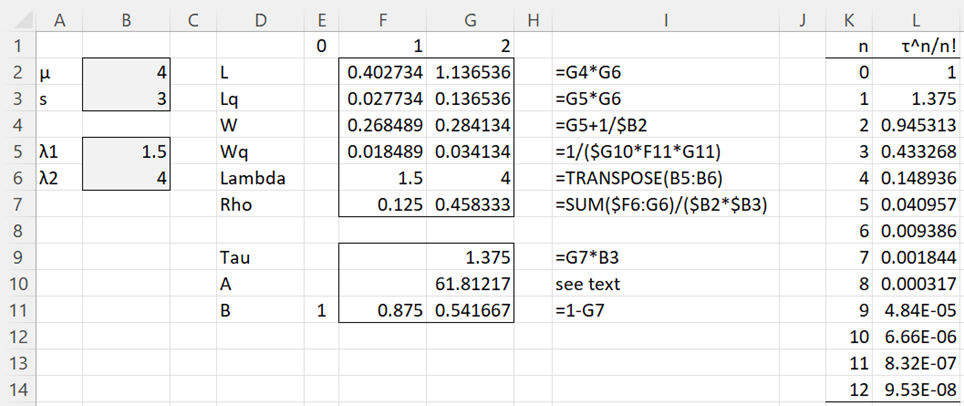
Example 1: Calculate L, Lq, W, and Wq for the M/M/s queueing model with two servers with two priority classes where the arrival rates and the service rate are as described in column B of Figure 1.
Figure 1 – M/M/s with non-preemptive priority
The results are shown on the right side of Figure 1. Column I displays the formulas in column G. The formula in cell G10 is
=FACT(B3)*(B3*B2-SUM(B5:B6))*SUM(OFFSET(L2,0,0,B3,1))/G9^B3+B3*B2
This formula references the values in column L. Here, cell L2 contains the formula =G$9^K2/FACT(K2), and similarly for the other cells in column L.
Worksheet Functions
Excel Function: The Real Statistics Resource Pack supports the following array function. Here, R1 is a row or column array or cell range that contains the arrival rates for the various priority classes.
MMsP(R1, μ, s, lab): returns an array with L, Lq, W, Wq, ρ for each priority class in an M/M/s non-preemptive priority queueing model with s servers, mean arrival rates in R1, and a mean service rate of μ.
If lab = TRUE (default FALSE) then an extra column of labels is appended to the output.
You can obtain the values in Figure 1 via the array formula =MMsP(B5:B6,B2,B3,TRUE).
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Ross, S. M. (2014) Introduction to probability models, 11th Ed. Academic Press
https://ebin.pub/introduction-to-probability-models-11nbsped-0124079482-9780124079489.html
Sztrik, J. (2021) Basic queueing theory
https://irh.inf.unideb.hu/~jsztrik/education/16/SOR_Main_Angol.pdf
Shores, T. S. (2017) Queueing theory basics and models
No longer available online
Hillier, F. S., Lieberman, G. J. (2010) Introduction to operations research. 9th Ed.
http://www.maths.lse.ac.uk/Personal/stengel/HillierLieberman9thEdition.pdf