Basic Concepts
The M/M/s/K queueing model is like the M/M/1/K model, except that there are s servers instead of 1.
It is sufficient to look at the case where s ≤ K (where K is the maximum size of the queue) since if K < s then at most K of the s servers will ever be used. Also note that when K = s, there is no queueing since customers who arrive either get serviced immediately or go away permanently.
Properties
This time, we see that the probability that no customers are in the system is given by the formula
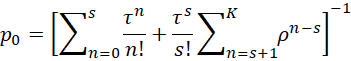
where ρ and τ are defined as in the M/M/s model. Thus for n = 0, 1, …, s
![]()
while for n = s, s+1, …, K, we have
![]()
and clearly pn = 0 for n > K. We also have for ρ ≠ 1
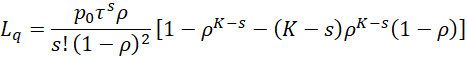
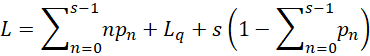
In general
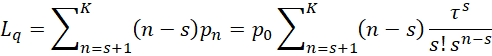
We can use this formula in the case where ρ = 1, in which case, τ = sρ = s. In this case, we also have
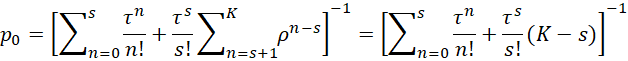
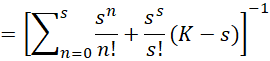
Little’s Law
As described in Queueing Theory, we can apply Little’s law to obtain the mean time that a customer remains in the system W and the mean time a customer waits in the queue Wq.
where (assuming s ≤ K)
![]()
Example
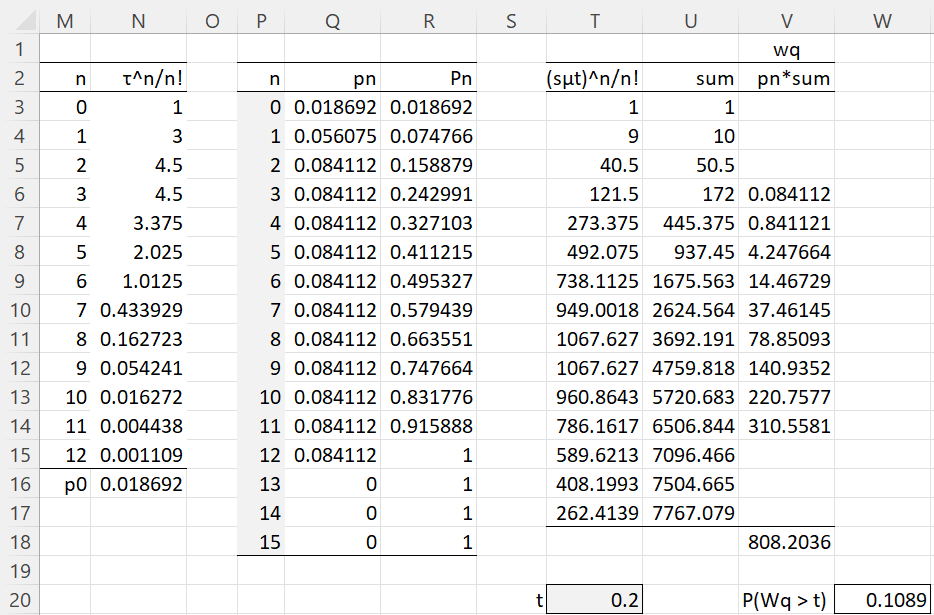
Example 1: Calculate the various parameters for an M/M/s/K queueing model with λ = 45, μ = 15, s = 3 servers, and a queue with the maximum capacity of K = 12.
The results are shown in Figure 1.
Figure 1 – M/M/s/K queueing model (part 1)
Here, cell G3 contains the formula
=N16*B6^B4/FACT(B4)*IF(G6=1,(B5-B4)*(B5-B4+1)/2,G6*(1-G6^(B5-B4+1)-(B5-B4+1)*G6^(B5-B4)*(1-G6))/(1-G6)^2)
You can calculate p0 in cell Q3 of Figure 2 by the formula =N16 and P0 in cell R3 by the formula =Q3. Here, cell N16 contains the formula
=1/(SUM(OFFSET(N3,0,0,B4,1))+B6^B4/FACT(B4)*IF(G6=1,B5-B4+1,(1-G6^(B5-B4+1))/(1-G6)))
where cell N3 contains =B$6^M3/FACT(M3), and similarly for the other formulas in N3:N15.
You can calculate the other pn and Pn values by placing the formula
=IF(P4>B$5,0,N$16*B$6^P4/IF(P4<B$4,FACT(P4),FACT(B$4)*B$4^(P4-B$4)))
in cell Q4 and =R3+Q4 in cell R4, and then highlighting Q4:R18, and pressing Ctrl-D.
Figure 2 – M/M/s/K queueing model (part 2)
Cell T4 contains the formula =(B$3*B$4*T$20)^P3/FACT(P4), U4 contains =U3+T4, and similarly for the other formulas in columns T and U.
Cell S4 contains the formula =IF(M4<B$4,N4*R4,””) and T4 contains =IF(M4<B$4,N4*R3,””), and similarly for the other formulas in columns S and T.
You can calculate the value of P(wq > t) in cell W20 for t = .2 (cell T20) via the formula =V18*EXP(-B3*B4*T20)/(1-OFFSET(Q3,B5,0,1,1)) where cell V18 contains the formula =SUM(V4:V17). Here, cell V3 contains the formula =IF(P3<B$4,””,IF(P3<B$5,Q3*OFFSET(U3,-B$4,0,1,1),””)), and similarly for the other formulas in V3:V17.
Worksheet Functions
Excel Functions: The Real Statistics Resource Pack supports the following array function.
MMsK(λ, μ, s, k, lab): returns a column array with the L, Lq, W, Wq, ρ, λ-bar for the M/M/s/K queueing model with parameters K = k, s, λ and μ.
If lab = TRUE (default FALSE) then an extra column of labels is appended to the output. In addition, the following non-array functions are also supported.
MMsKPn(λ, μ, s, k, n, cum) = pn for the M/M/s/K queueing model defined by K = k, s, λ, and μ if cum = FALSE (default) and Pn otherwise.
MMsKWq(λ, μ, s, k, t) = P(wq > t) for the M/M/s/K queueing defined by K = k, s, λ, and μ
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Ross, S. M. (2014) Introduction to probability models, 11th Ed. Academic Press
https://ebin.pub/introduction-to-probability-models-11nbsped-0124079482-9780124079489.html
Sztrik, J. (2021) Basic queueing theory
https://irh.inf.unideb.hu/~jsztrik/education/16/SOR_Main_Angol.pdf
Shores, T. S. (2017) Queueing theory basics and models
No longer available online