Basic Concepts
This model is like the M/M/1 model with non-preemptive priority queueing (with a service rate of μ no matter the priority class) except that when a customer arrives with a higher priority than a customer being served, then this customer must leave the server to be replaced by the new customer (with higher priority) that just arrived.
The customer who has been bumped returns to the front of the queue and will be serviced next unless there is some other customer in the queue with a higher priority.
Properties
For this model, the average time that a customer from priority class k remains in the system is Wk, and the mean time queueing Wqk are given by
where the Bk are as described in M/M/1 model with non-preemptive priority queueing.
Note that pre-emption does not affect the mean server time, which remains 1/μ for all customers no matter their priority class. Also since the service rate is exponential, there is no memory of a previous time in the server for a pre-empted customer.
Using Little’s Law
Example
Example 1: Repeat Example 1 from M/M/1 model with non-preemptive priority queueing but using preemptive priority queueing.
The result is shown on the right side of Figure 1. Column J contains the formulas used in column H.
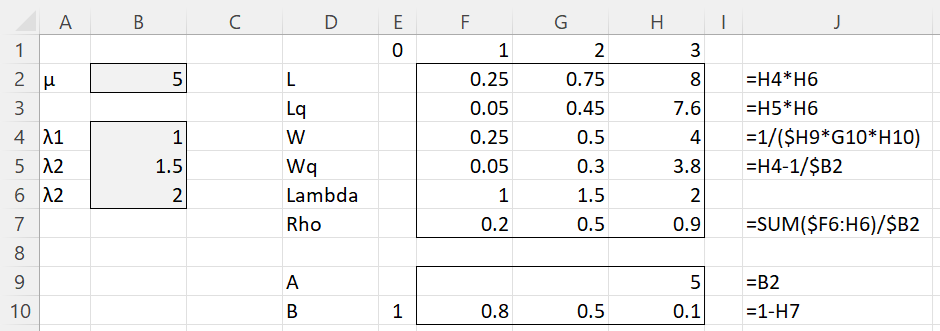
Figure 1 – M/M/1 with preemptive priority queueing
Worksheet Function
Excel Function: The Real Statistics Resource Pack supports the following array function. Here, R1 is a column or row array or cell range containing the mean arrival rates for the various priority classes.
MM1PP(R1, μ, lab): returns an array with L, Lq, W, Wq, ρ for each priority class in an M/M/1 model with pre-emptive priority queueing with mean arrival rates described in R1 and a mean service rate of μ.
If lab = TRUE (default FALSE) then an extra column of labels is appended to the output.
You can obtain the values in Figure 1 via the array formula =MM1PP(B4:B6,B2,TRUE).
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Ross, S. M. (2014) Introduction to probability models, 11th Ed. Academic Press
https://ebin.pub/introduction-to-probability-models-11nbsped-0124079482-9780124079489.html
Sztrik, J. (2021) Basic queueing theory
https://irh.inf.unideb.hu/~jsztrik/education/16/SOR_Main_Angol.pdf
Shores, T. S. (2017) Queueing theory basics and models
No longer available online
Hillier, F. S., Lieberman, G. J. (2010) Introduction to operations research. 9th Ed.
http://www.maths.lse.ac.uk/Personal/stengel/HillierLieberman9thEdition.pdf