Basic Concepts
We describe an M/M/1 queueing model where the customer base is partitioned into a finite number of priorities. A higher-priority customer gets serviced before a lower-priority customer. If there is more than one such customer, the first in the queue gets service. Once a customer is in the server it won’t get bumped even if a higher priority customer arrives.
The arrival rates for the various priority classes can be different, although the service rates will all be the same, denoted μ.
Suppose that you have m priority classes 1, 2, …, m with 1 higher priority than 2, etc. Suppose too that the arrival rates for these priority classes are λ1, λ2, …, λm. Thus, the total arrival rate is λ = λ1 + λ2 + … + λm, and so the utility is ρ = λ/μ. A steady state is achieved when ρ < 1.
Properties
For k = 1, 2, …, m
where
From these, we derive
Example
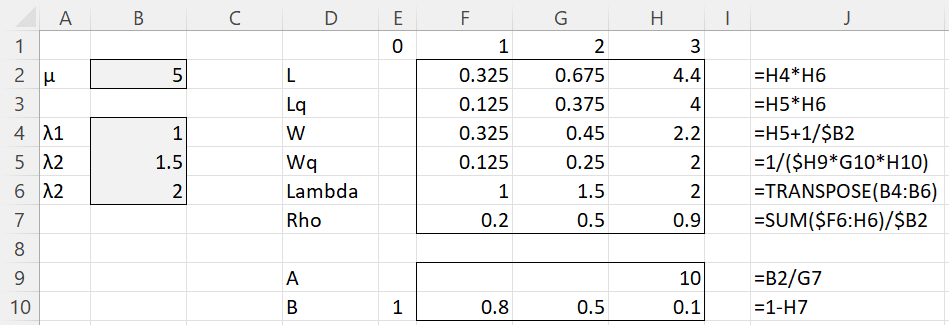
Example 1: Calculate L, Lq, W, and Wq for each of the priority classes where the arrival rates for each of the 3 priority classes and the service rate are as described in column B of Figure 1.
Figure 1 – M/M/1 with non-preemptive priority
The results are shown on the right side of Figure 1. Column J displays the formulas in column H. Note that λ = 1+1.5+2 = 4.5.
Worksheet Functions
Excel Function: The Real Statistics Resource Pack supports the following array function. Here, R1 is a row or column array or cell range that contains the arrival rates for the various priority classes.
MM1P(R1, μ, lab): returns an array with L, Lq, W, Wq, ρ for each priority class in an M/M/1 non-preemptive priority queueing model with the mean arrival rates in R1 and mean service rate of μ.
If lab = TRUE (default FALSE) then an extra column of labels is appended to the output.
You can obtain the values in Figure 1 via the array formula =MM1P(B4:B6,B2,TRUE).
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Ross, S. M. (2014) Introduction to probability models, 11th Ed. Academic Press
https://ebin.pub/introduction-to-probability-models-11nbsped-0124079482-9780124079489.html
Sztrik, J. (2021) Basic queueing theory
https://irh.inf.unideb.hu/~jsztrik/education/16/SOR_Main_Angol.pdf
Shores, T. S. (2017) Queueing theory basics and models
No longer available online
Hillier, F. S., Lieberman, G. J. (2010) Introduction to operations research. 9th Ed.