M/G/infinity Queueing Model

Basic Concepts

Here we assume that there are an infinite number of servers and so customers are immediately served without waiting in a queue. This model is useful when you want to explore a situation where customers don’t need to wait for service (or at least rarely wait for service). Let τ = λ/μ. Then

L_q = 0          W_q = 0

L = τ          W = 1/μ

p₀ = e^-τ          p_n = p₀τⁿ/n!

Since L has a Poisson distribution, P(l > t) = P(service time > t). Also var(l) = τ.

Example

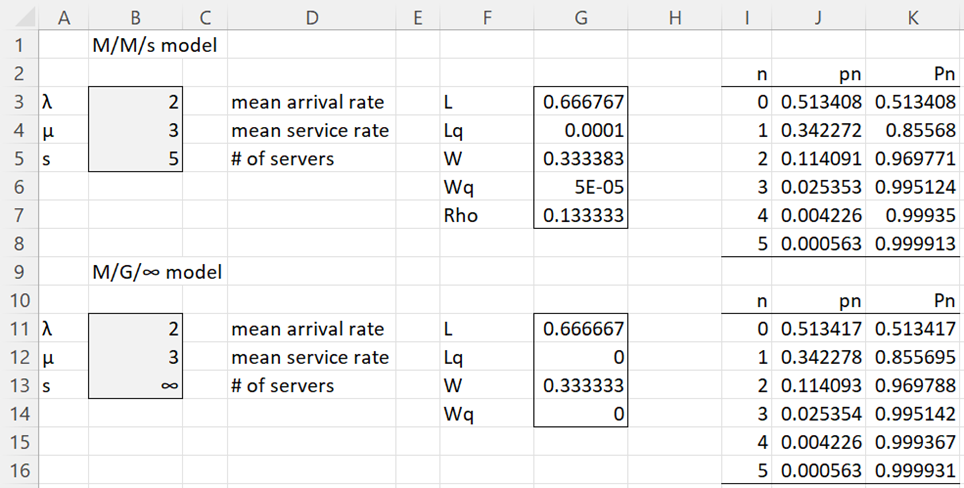
Example 1: In Figure 1 we compare an M/G/∞ model with an M/M/s model. We see that even when the number of servers is s = 5, the two models, at least in this case, are fairly similar.

Figure 1 – M/G/∞ model comparison

In general, you need to find a value of s sufficiently large to obtain an M/M/s model that is equivalent to a specified M/G/∞ model.

Worksheet Functions

Excel Functions: The Real Statistics Resource Pack supports the following array function.

MGinf(λ, μ, lab): returns a column array with L, L_q, W, W_q for the M/G/∞ queueing model with exponential arrivals with a mean arrival rate of λ and a general service distribution with a mean service rate of μ.

If lab = TRUE (default FALSE) then an extra column of labels is appended to the output. 

The following non-array function is also supported:

MGinfPn(λ, μ, n, cum) = p_n for the M/G/∞ queueing model defined by λ and μ if cum = FALSE (default) and P_n otherwise.

You can obtain the values in range F11:G14 of Figure 1 via the array formula =MGinf(B11,B12,TRUE). To obtain the p_n values for the M/G/∞ model in Figure 1, place the formula =MGinfPn(B11,B12,I11) in cell J11, highlight J11:J16, and press Ctrl-D. You can obtain the P_n values by placing =MGinfPn(B11,B12,I11,TRUE) in cell K11, highlighting K11:K16, and pressing Ctrl-D.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Ross, S. M. (2014) Introduction to probability models, 11th Ed. Academic Press
https://ebin.pub/introduction-to-probability-models-11nbsped-0124079482-9780124079489.html

Sztrik, J. (2021) Basic queueing theory
https://irh.inf.unideb.hu/~jsztrik/education/16/SOR_Main_Angol.pdf

Shores, T. S. (2017) Queueing theory basics and models
No longer available online

Güneş, M. (2023) Queueing models
https://www.mi.fu-berlin.de/inf/groups/ag-tech/teaching/2013_SS/L_19540_Modeling_and_Performance_Analysis_with_Simulation/08.pdf