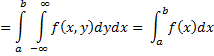The following are some advanced concepts associated with continuous distributions and requiring calculus. Occasionally we also include the discrete version of the same concept (at least where this concept isn’t already covered in Discrete Probability Distributions).
Probability Density and Distribution Functions
Definition 1: For a continuous random variable x, f is a frequency function, also called the probability density function (pdf), provided:
![]()
![]()
for all a < b in the range of x.
The corresponding (cumulative) distribution function is defined by
Property 1: For continuous random variables
![]()
Property 2: For continuous random variables
![]()
Joint Density and Distribution Functions
Definition 2: If x and y are discrete random variables then the (joint) frequency function (or probability density function) f of x and y is defined as follows:
For continuous random variables:
![]()
![]()
The corresponding joint cumulative distribution function F is:
Definition 3: The random variables x and y are independently distributed if there are functions g and h such that
These definitions and properties can be extended to n random variables.
Marginal Distribution Functions
Definition 4: If f(x,y) is the joint frequency function of discrete random variables x and y, the marginal frequency functions f(x) and g(y) are defined by
![]() Thus, f(a) = P(x = a) and g(b) = P(y = b). Note that for simplicity we use the letter f for both the joint frequency function and the marginal frequency function of the first variable.
Thus, f(a) = P(x = a) and g(b) = P(y = b). Note that for simplicity we use the letter f for both the joint frequency function and the marginal frequency function of the first variable.
Definition 5: If f(x, y) is the joint frequency function of continuous random variables x and y, the marginal frequency functions f(x) and g(y) are defined by
![]() Property 3: For a continuous random variable x
Property 3: For a continuous random variable x
![]()
A similar property holds for g(y).
Property 4: The marginal frequency functions are indeed frequency functions.
Proof: We need to show
![]()
![]()
for all a < b in the range of x (and similarly for g(y)). The first of these comes from the definition of a marginal frequency function and a similar property of the joint frequency function. The last two results from Property 3.
Conditional Distribution Functions
Definition 6: If f(x, y) is the joint frequency function of random variables x and y, the conditional frequency functions f(y|x) and g(x|y) are defined by
![]() where f(x) and g(y) are not zero.
where f(x) and g(y) are not zero.
Observation: In the discrete case, f(b|a) = P(y = b | x = a) and g(a|b) = P(x = a | y = b)
Property 5: The conditional frequency functions are frequency functions
Proof: We view f(y|x) as a function of y where x is held fixed. In the continuous case, we need to show three things when f(x) ≠ 0:
![]()
![]()
Since f(y|x) = f(x, y)/f(x) the first of these is a consequence of the fact that f(x) > 0 and f(x, y) ≥ 0 since these are frequency functions. Now, since x is held fixed
![]()
which shows that the second property is true (setting a = ∞ and b = –∞).
Property 6: If f(x, y) is the joint frequency function of random variables x and y, with the marginal and conditional frequency functions f and g as defined above, then
Proof: This is a trivial consequence of the definition of f(y|x) and g(x|y).
Property 7: If x has frequency function f(x) and y has frequency function g(y), and x and y are independently distributed, then f(x) = f(x|y) and g(y) = g(y|x).
Proof: By the definition of f(x|y)
By definition of independence,
Combining these two equations and dividing by f(x), we have the desired result, assuming f(x) > 0.
References
Bass, R. F. et al. (2013) Upper level undergraduate probability with actuarial and financial applications
https://probability.oer.math.uconn.edu/wp-content/uploads/sites/2187/2020/03/OERprobability2020.pdf
Navidi, W. (2011) Statistics for engineers and scientists (3rd ed) McGraw Hill