Continuous Probability Distributions

Basic Concepts

We now extend the definition of probability distribution from discrete (see Discrete Probability Distributions) to continuous random variables. Such variables take on an infinite range of values even in a finite interval (e.g. weight of rice, room temperature, etc.).

For a discrete random variable x, the probability that x assumes a value between a and b (exclusive) is expressed by

For a continuous random variable, however, the frequency function f (more commonly referred to as the probability density function) can assume an infinite number of values (even in a finite interval). Thus, we can’t simply sum up the values in the ordinary way. For continuous variables, the equivalent formulation is that the probability that x assumes a value between a and b is given by

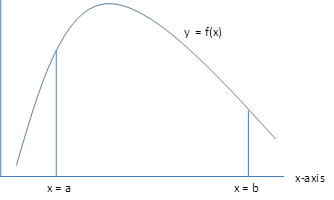
i.e. the area under the graph of y = f(x) bounded by the x-axis and the lines x = a and x = b.

Figure 1 – Area under the curve

Definition and Key Property

Definition 1: For a continuous random variable f(x) is a frequency function, more commonly called the probability density function (pdf) provided:

The corresponding (cumulative) distribution function (cdf) F(x)  is defined by

Property 1: For any continuous random variable x with distribution function F(x)

Observations

f is a valid probability density function provided that f always takes non-negative values and the area between the curve and the x-axis is 1. f is the probability density function for a particular random variable x provided the area of the region indicated in Figure 1 represents the probability that x assumes a value between a and b inclusively.

Note that the probability that f takes any particular value a is not f(a). In fact for any specific value a, the probability that x takes the value a is considered to be 0.

Essentially the area under a curve is a way of summing when dealing with an infinite range of values in a continuum. For those of you familiar with calculus

Click here for additional information about continuous probability distributions which relies on calculus.

We will study a number of continuous distributions in this website such as the normal distribution and t distribution.

References

Bass, R. F. et al. (2013) Upper level undergraduate probability with actuarial and financial applications
https://www.math.union.edu/~marianop/MATH3371f19/ProbText.pdf

Navidi, W. (2011) Statistics for engineers and scientists (3rd ed) McGraw Hill