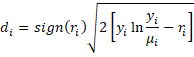Poisson Regression Residuals and Goodness of Fit

Types of Residuals

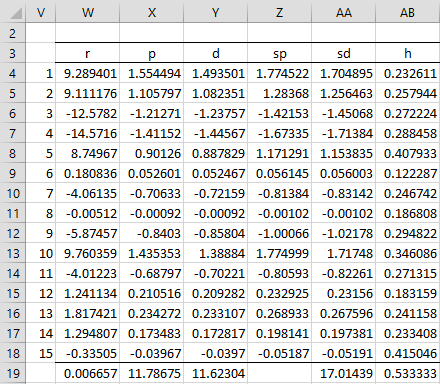
As for multiple linear regression, various types of residuals are used to determine the fit of the Poisson regression model. These are described in Figure 1. Each residual is calculated for every observation. Figure 1 also shows the Excel formula used to calculate each residual for the first observation (corresponding to row 4 of Figure 1 of Poisson Regression using Solver) in Example 1 of Poisson Regression using Solver. All the residual values for Example 1 are shown in Figure 2.

Residual	Formula	Cell	Excel Formula
Raw residual		W4	=J4-Q4
Pearson residual		X4	=W4/SQRT(Q4)
Deviance residual		Y4	=SIGN(W4)*SQRT(2*(J4*LN(J4/Q4)-W4))
Studentized Pearson res.		Z4	=Y4/SQRT(1-AB4)
Studentized deviance res.		AA4	=Z4/SQRT(1-AB4)

Figure 1 – Types of residuals

Observations

Since the variance and the mean are equal for a Poisson distribution, the Pearson residuals standardize the raw residuals by dividing them by the standard deviation. If there is overdispersion, we can elect to use a corrected Pearson residual, namely

The Studentized residuals reference the h_ii values on the main diagonal of the hat matrix. The hat matrix is defined by the formula

where V is the diagonal matrix whose main diagonal contains the values μ_i (with zeros elsewhere). Actually, this is equivalent to the simpler formula

where Z is the n × k matrix [z_ij] and z_ij =μ_i·x_ij. Thus, the diagonal of the hat matrix for Example 1 of Poisson Regression using Solver (i.e. range AB4:AB18 of Figure 6 of Poisson Regression using Solver) can be calculated by the Real Statistics array formula

=DIAG(MMULT(MMULT(Q4:Q18*F4:I18, MINVERSE(MMULT(TRANSPOSE(F4:I18),Q4:Q18*F4:I18))), TRANSPOSE(F4:I18)))

A summary of the various residuals for Example 1 of Poisson Regression using Solver is shown in Figure 2.

Figure 2 – Residuals for Poisson Regression example

Interpretation

The values on the main diagonal of the hat matrix characterize the influence that each observation has on the regression model (i.e. on the coefficients of the model). A rule of thumb is that values for which h_ii > 2k/n have a large influence on the model.

For Example 1 of Poisson Regression using Solver, this cutoff is 2k/n = .5333 (cell AB19 of Figure 2). Note that none of the hat values in range AB4:AB18 exceed this value.

Also note that the sum of the raw residual values is .006657 (cell W19), which is close to zero, as we would expect.

Residual Plots

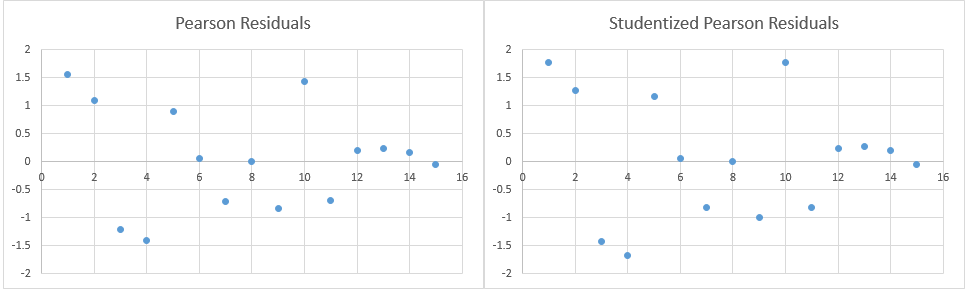
We can create various residual plots (see Figure 3). These plots should show random patterns and can be useful in identifying outliers or observations with high influence.

Figure 3 – Residual plots

Goodness-of-fit

Besides characterizing the contribution of each observation to the regression model, these residuals are used to define two measures of the overall fit of the model, as shown in Figure 4.

Figure 4 – Goodness of Fit

The Pearson goodness of fit statistic (cell B25) is equal to the sum of the squares of the Pearson residuals, i.e.

This can be calculated in Excel by the formula =SUMSQ(X4:X18). We can use P to test the goodness of fit, based on the fact that P ∼ χ²(n–k) when the null hypothesis that the regression model is a good fit is valid. As we can see in cell C25, p-value = CHISQ.DIST.RT(11.78675,15-3) = 0.379884 > .05 = α, and so we have no reason to reject the goodness of fit of the Poisson regression model for Example 1.

Note that phi is simply Pearson’s goodness of fit statistic divided by n – k, as shown in cell B29. When P and, therefore phi is too high, then the model won’t be a good fit.

The  goodness of fit statistic (cell B26) is equal to the sum of the squares of the deviance residuals, i.e.

G² can be calculated in Excel by the formula =SUMSQ(Y4:Y18). We can also use G² to test the goodness of fit, based on the fact that G² ∼ χ²(n–k) when the null hypothesis that the regression model is a good fit is valid. The p-value for this test is shown in cell C26.

AIC

We define Akaike’s Information Criterion (AIC) for Poisson Regression models by

This is a useful measure of fit when comparing competing models, giving some weight to the number of independent variables. For Example 1 of Poisson Regression using Solver, AIC = 19.623 is computed using the formula =B26+2*N5 as shown in cell B28 of Figure 4.

Note that if we drop the psychological profile variables (Psy A and Psy B), our model would contain only one independent variable (k = 1) instead of three (k = 3). In this case,  the model would no longer be a good fit (G² = 107.3237 and p-value = 6.24E-17) and AIC would rise to 111.324.

Note, however, that, in general, it is entirely possible that removing one or more independent variables could result in a model that is still a good fit but with a lower AIC indicating that the model with fewer independent variables is better. In this case, the premium that AIC places on fewer variables is more than offset by the higher value for G².

As we have seen when studying logistic regression (see Comparing Logistic Regression models), with nested models, we can perform a chi-square test to compare models, i.e. to determine whether the larger model is significantly different from the smaller model, namely by using the test

2(LL₁ – LL₀) ~ χ²(df₁ – df₀)

As we have seen, for Example 1 of Poisson Regression using Solver, LL₁ = -48.8017 with df₁ = 13. For the Poisson regression model where we remove the psychological profile variables, we would get LL₀ = -96.6521 with df₀ = 11. Thus for the chi-square test, p-value = CHISQ.DIST.RT(95.70067,2) = 1.66E-21, which shows there is a significant difference between the models with and without the psychological profiles.

Pseudo R²

The pseudo R² statistic plays a role similar to that of R² in multiple linear regression. This statistic is defined by

where

and

Note too that LL_min can also be expressed as

Here, the t_i refer to the population values in column B of Figure 1 (or column K of Figure 2) of Poisson Regression using Solver.

For Example 1 of Poisson Regression using Solver, LL_min is calculated in cell N13 of Figure 2 of that webpage using the formula =U19-(1-LN(N11))*J19-S19, where U19 contains the formula =SUM(U4:U18), J19 contains the formula =SUM(J4:J18), S19 contains the formula =SUM(S4:S18) and N11 contains the formula =J19/K19. Similarly, LL_max is calculated in cell N15 of Figure 2 of that webpage using the formula =T19-J19-S19.

R² is calculated in cell N16 of that webpage by the formula =(N14-N13)/(N15-N13) and has the value 0.96425, which is almost 1, indicating an almost perfect fit.

There are many other commonly used formulas for the pseudo R² statistic. The McFadden R² statistic is calculated by

which for Example 1 Poisson Regression using Solver takes the value 1 – (-48.8017)/(-204.985) = 0.761925.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Hintze, J. L. (2007) Poisson regression. NCSS
https://www.ncss.com/wp-content/themes/ncss/pdf/Procedures/NCSS/Poisson_Regression.pdf

Nussbaum, E. M., Elsadat, S., Khago, A. H. (2007) Best practices in evaluating count data, Chapter 21: Poisson regression.
http://www.academia.edu/438746

Penn State (2017) Poisson regression. STAT 504: Analysis of discrete data.
https://online.stat.psu.edu/stat504/lesson/9