Random Effects Model (REM)

The fixed-effects panel data models are designed to work properly even when the unobserved time-invariant ui is correlated with one or more of the independent variables. We now describe the random-effects model that is only appropriate when the unobserved time-invariant ui is not correlated with any of the independent variables.

Topics

Basic Concepts

We consider the regression model

Panel data regression model

There are k regressors, xitj, which can potentially vary by unit (represented by the i subscript) and time period (represented by the t subscript) plus an unobserved time-invariant effect ui, an intercept, and an error term eit. We will assume that there are p time periods and n units. In addition, we assume that there are no missing time periods (a balanced model), and so there are np rows of data.

We can assume without loss of generality that the mean of the ui is zero (by subtracting the mean from the intercept coefficient b0.

For the random-effects model, we further assume that the ui are uncorrelated with the xitj, namely

REM correlation assumption

As a result, we can use the regression model

Regression model composite error

using the composite error term vit = ui + eit. OLS regression is now suitable, except that the vit are serially correlated across time. In fact, for t ≠ s

Covariance of composite errors

where

Error components

We can use the Feasible Generalized Least-Squares (FGLS) regression in this case. This is what is known as the random-effects model (REM). This approach has good properties when the sample size n is large, and the number of time periods p is relatively small.

Transformation

In particular, we will use the transformation parameter

REM transformation parameter

to obtain the transformed regression model

Transformed regression model

where each variable is quasi-demeaned. It turns out that the errors in this model are serially uncorrelated. Note that once theta is known, this model can be created using the PANEL_DEMEAN function described in Demeaning for Panel Data by setting the weight parameter to theta.

The random-effects model includes support for time-invariant independent variables xij (i.e. where xitj = xisj for all times t, s).

To use this model, we need estimates for σe2 and σu2. These are obtained using the Swamy-Arora method, as follows.

We can obtain an estimate for σe2 by performing OLS regression on the demeaned data as described in Demeaning for Panel Data. The corrected MSRes value from this regression then serves as the estimate for σe2 (it is not necessary to correct the standard errors of the regression coefficients).

We next estimate σu2 by performing OLS regression on the data for the unit means to obtain MSRes for this regression. We then use the estimate σu2 = σe2 – MSRes/p where p = the number of time periods.

Observations

Note that when θ = 0, the REM is equivalent to the Pooled OLS model. When θ = 1, REM is equivalent to the FEM. If θ is close to 0, then ui is relatively unimportant (since σu2 is small relative to σe2). Usually, though, θ is close to 1 and so σu2 is large relative to σe2.

When θ is close to 1, the bias in the REM estimate is low, while when θ is close to 0, the bias is larger (i.e. the unobserved effect makes up a larger portion of the error term). Note too that as p → ∞, θ → 1, in which case, the REM and FEM produce similar estimates.

References

Gujarati, D. & Porter, D. (2009) Basic econometrics. 5th Ed. McGraw Hill
http://www.uop.edu.pk/ocontents/gujarati_book.pdf

Hill, R. C., Griffiths, W. E., Lim, G. C. (2018) The principles of econometrics. 5th edition. Wiley.
https://books.google.it/books?hl=en&lr=&id=LnNdDwAAQBAJ&oi=fnd&pg=PR26&dq=Hill,+R.+C.,+Griffiths,+W.+E.,+Lim,+G.+C.+(2018)+The+principles+of+econometrics.+5th+edition.+Wiley.&ots=Sfzb6K2oM6&sig=Z-1FvlvlrAwGcLYLCG80KXadQms#v=onepage&q&f=false

12 thoughts on “Random Effects Model (REM)”

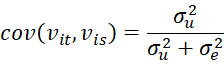
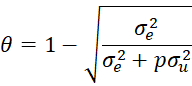
  1. Thanks so much for creating this software!

    I had a question about the equation just below the sentence “OLS regression is now suitable, except that the vit are serially correlated across time.” Instead of “cov”, shouldn’t it be “corr” for “correlation”?

    Reply

  2. Hi Charles,

    I’ve noticed that the REM analysis tool does not provide the option of generating heteroscedasticity robust standard errors.

    Is that deliberate? I.e. is the quasi-demeaning methodology not amenable to generating robust SEs? Or alternatively, is heteroskedasticity accounted for via theta?

    Thank you,

    Gareth

    Reply

    • Hi Gareth,
      I don’t see why you wouldn’t be able to use robust standard errors. After the transformation described on the website you could use the robust errors capability from the Regression data analysis tool. Real Statistics doesn’t (yet) support this via the Panel Analysis data analysis tool.
      Charles

      Reply

  3. Hello Charles,

    In my use of the panel data demeaning function (PANEL_DEMEAN) I have found that – as I would expect – a single observation takes a value of zero once it is demeaned. Hence, single observations cannot be included in a FEM, or alternatively they are automatically excluded from the calculation of the regression parameters.

    For REM, the model shown under the ‘Transformations’ heading above suggests that the mean of a single observation – which takes a value of zero – is multiplied with theta so that it should also take a value of zero. However, in my use of the random effects function (PANEL_REM), when single observations are quasi-demeaned they do not take a value of zero.

    Can you confirm whether or not this is correct? Is the order of operations different from that which is depicted in the model?

    Thank you,

    Gareth

    Reply

  4. Hi Charles,

    I’m looking forward to seeing the Hausman test in the next release of XrealStats!

    Best Regards,

    Gareth

    Reply

  5. Hi Charles,

    In regards to the text above that reads: “Note that when θ = 0, the REM is equivalent to the Pooled OLS model. When θ = 0, REM is equivalent to the FEM.”

    Should it not instead read as follows: “Note that…When θ = 1, REM is equivalent to the FEM.”?

    The difference being θ = 1 (as opposed to 0).

    Best Regards,

    Gareth

    Reply

Leave a Comment