Basic Concepts
We use Hausman’s test, aka Durbin-Wu-Hausamn’s (DWH) test, to determine if a fixed-effects or random-effects model is a better fit for your panel data.
Suppose that B1 is the REM estimate for the coefficients of the linear regression model y = βX + ε and B0 is the FEM estimate for the coefficients. We want to test the hypothesis
H0: B0 and B1 are consistent, but B1 is efficient and B0 is not
H1: B0 is consistent, but B1 is not
Recall that an estimator is consistent means that the estimate improves as the sample size increases. An estimator is efficient if its asymptotic variance is smaller than any other estimator.
Test
To conduct the test, create a new, augmented regression model consisting of the independent variables from the REM and FEM (demean) models and the dependent variable from the REM. The test statistic is then
where k = the number of independent variables represented by the data, n = dfTREM – 1 = the sample size (# of rows of data) and SSE refers to the sum of squares for the error term (residuals).
Example
Example 1: Carry out Haussman’s test for the data in Example 1 of REM Example and Functions.
Range AG3:AL27 of Figure 1 displays the data for the augmented regression model. The first two columns come from the FEM, as shown in range R1:S25 of Figure 2 of Demeaning for Panel Data. The next four columns come from the REM, as shown in range AI1:AL25 of Figure 2 of REM Example and Functions. From this figure we also see that k = 3-1 = 2 (cell AO12), n = 24 (AO14) and SSEREM = 1.26696 (AP13). These values are copied into cells AW9, AW5, and AW6 of Figure 1 below, respectively.
Figure 1 – Augmented regression + Hausman’s test
The left side of Figure 1 shows the data for the augmented regression model. Using ordinary multiple linear regression without an intercept on the data in AG3:AL27, we obtain SSEAug = .71744 (cell AP15), which we copy into cell AW7. We can now calculate H = 18.365 (cell AW8) using the formula =AW5*(AW6-AW7)/AW7. We obtain p-value = .000103 (cell AW10) via the formula =CHISQ.DIST.RT(AW8,AW9).
Since we have a significant result, we favor the FEM model over the REM model.
Worksheet Function
Real Statistics Function: The Real Statistics Resource Pack provides the following worksheet function where R1 contains balanced panel data sorted first by unit and then by time period (as in range C2:E25 of Figure 1 of REM Example and Functions).
HAUSMAN(R1, periods, lab): returns a column array with the values H, df, p-value for Hausman’s test on the data in R1 based on periods number of time periods per unit. If lab = TRUE then a column of labels is appended to the output (default FALSE).
For the data in range C2:E25 of Figure 1 of REM Example and Functions, the formula =HAUSMAN(C2:E25,3,TRUE) produces the output shown in range AV8:AW10 of Figure 1.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Cottrell, A., Lucchetti, R. (2023) Gretl user’s guide
https://gretl.sourceforge.net/gretl-help/gretl-guide.pdf
Wikipedia (2013) Durbin-Wu-Hausman test
https://en.wikipedia.org/wiki/Durbin%E2%80%93Wu%E2%80%93Hausman_test#:~:text=The%20Hausman%20test%20can%20be,as%20consistent%20and%20thus%20preferred
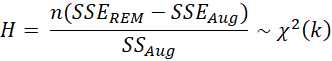

Bravo Charles!
I hope you are handsomely rewarded for your social contribution, you’re a scholar and a saint.
Thank you,
Gareth
Hi Gareth,
Glad that you like the late addition to Release 8.7. I was quite pleased to be able to add it to the release.
Charles