Derivation of Spline Polynomials

Spline fitting or spline interpolation is a way to draw a smooth curve through n+1 points (x₀, y₀), …, (x_n,y_n). Thus, we seek a smooth function f(x) so that f(x_i) = y_i for all i. In particular, we seek n cubic polynomials p₀, …, p_n-1 so that f(x) = p_i(x) for all x in the interval [x_i, x_i+1].

Key Property

Property 1: The cubic polynomials that we are seeking can be defined by

p_i(x) = a_i(x–x_i)³ + b_i(x–x_i)² + c_i(x–x_i) + d_i

where for i = 0, …, n-1

based on h_i = x_i+1 – x_i and k_i = y_i+1 – y_i. The b_i coefficients are defined via matrix operations as follows. First define for i = 1, …, n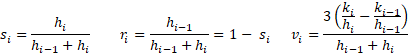

Now define U = [u_ij] to be an n+1 × n+1 matrix (where i, j = 0, …, n) where

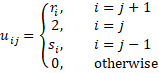
and define B = [b_i] and V = [v_i] to be n+1 × 1 matrices where the v_i are as defined above and B is defined by

B = U^-1V

Proof

The proof uses calculus.

We define n cubic polynomials p₀, …, p_n-1 with the following properties:

1. p_i(x) = a_i(x–x_i)³ + b_i(x–x_i)² + c_i(x–x_i) + d_i for all i = 0, …, n–1
2. if x_i-1 ≤ x ≤ x_i then f(x) = p_i(x) for all i = 0, …, n–1 (f defined piecewise by the p_i)
3. f(x_i) = y_i for all i = 0, …, n (points (x_i, y_i) lie on the y = f(x)  curve)
4. p_i-1 (x_i) = p_i (x_i) for all i = 0, …, n–1 (f  is continuous)
5. p′_i-1 (x_i) = p′_i (x_i) for all i = 0, …, n–1 (f′ exists and is continuous)
6. p′′_i-1 (x_i) = p′′_i (x_i) for all i = 0, …, n–1 (f′′ exists and is continuous)
7. p′′₀ (x₀) = 0 and p′′_n-1 (x_n) = 0 (initial conditions)

We also define h_i = x_i+1 – x_i and k_i = y_i+1 – y_i for i = 0, …, n–1.

By 1, 2, and 3, for i = 0, …, n–1

and so by 1, 3, and 4, for i = 0, …, n–1

or equivalently

By 1

and so

It now follows by 6 that

and so for i = 0, …, n–1

It now follows that

Solving for c_i it follows that

As we have seen previously

and so

It now follows by 5 that

or equivalently for i = 0, …, n–1

This can be re-expressed as

We now have n+1 linear equations in n+1 unknowns as follows for i = 1, …, n–1

Dividing both sides of this last equation by h_i-1 + h_i, we obtain the equivalent form

where r_i, s_i, and v_i are defined as in the statement of the property. With B, U, and V defined as in the statement of the property, the n+1 linear equations can be re-expressed as

UB = V

from which it follows that B = U^-1V, which completes the proof.

References

Chen, M-Q (2013) Cubic spline interpolation
This paper has been removed from the Internet

Jameson, A. (2019) Cubic splines
http://aero-comlab.stanford.edu/Papers/splines.pdf

Wang, K. (2013) A study of cubic spline interpolation
https://www2.rivier.edu/journal/ROAJ-Fall-2013/J784-Wang_cubic-splines.pdf