Spline Fitting and Interpolation

Basic Concepts

Spline fitting or spline interpolation is a way to draw a smooth curve through n+1 points (x₀, y₀), …, (x_n,y_n). Thus, we seek a smooth function f(x) so that f(x_i) = y_i for all i. In particular, we seek n cubic polynomials p₀, …, p_n-1 so that f(x) = p_i(x) for all x in the interval [x_i, x_i+1].

Property 1: The polynomials that we are seeking can be defined by

p_i(x) = a_i(x–x_i)³ + b_i(x–x_i)² + c_i(x–x_i) + d_i

where for i = 0, …, n-1

based on h_i = x_i+1 – x_i and k_i = y_i+1 – y_i. The b_i coefficients are defined via matrix operations as follows. First define for i = 1, …, n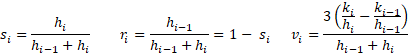

Now define U = [u_ij] to be an n+1 × n+1 matrix where i, j = 0, …, n and

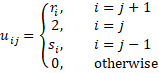
and define B = [b_i] and V = [v_i] to be n+1 × 1 matrices where the v_i are as defined above and B is defined by

B = U^-1V

Proof: See Derivation of Spline Polynomials. The proof uses calculus.

Example

Example 1: Create a spline curve that passes through the four points in range B4:C7 of Figure 1.

The coefficients for the three cubic polynomials p₀, p₁ and p₂ are shown in range B16:E18 of Figure 1. We show how to calculate these parameters in the rest of the figure.

Figure 1 – Spline curve calculation

Figure 2 displays some of the representative formulas in Figure 1.

Cells	Entity	Formula
B4	x0	input data
C4	y0	input data
F4	h0 = x1 – x0	=B5-B4
G4	h0 + h1	=F4+F5
H4	k0 = y1 – y0	=C5-C4
I4	k0/h0	=H4/F4
B11	u10 = h0/(h0 + h1)	=F4/G4
C11	u11 = 2	2
D11	u12 = 1 – u10	=1-B11
E11	u13 = 0	0
G11	v1 = 3(k1/h1–k0/h0)/(h0+h1)	=3*(I5-I4)/G4
I10:I13	B	=MMULT(MINVERSE(B10:E13),G10:G13)
B17	a1 = (b2 – b1)/(3h1)	=(I12-I11)/(3*F5)
C17	b1	=I11
D17	c1 = k1/h1 – h1(b2+2b1)/3	=I5-F5*(I12+2*I11)/3
E17	d1 = y1	=C5

Figure 2 – Representative formulas from Figure 1

We see from Figure 1, for example, that the second of the spline polynomials is

p₁(x) = .000774x³ – .01747x² + .196109x + 1.791759

Now the spline function f(x) = p₀(x) for x in the interval [2, 5], f(x) = p₁(x)  for x in the interval [5,13] and f(x) = p₂(x) for x in the interval [13, 15]. We capture this for the values of x between 2 and 15 in Figure 3.

Figure 3 – Spline curve fit

Here, we placed the formula =B$16*(K4-B$4)^3+C$16*(K4-B$4)^2+D$16*(K4-B$4)+E$16 in cell L4. We then highlighted the range L4:L6 and pressed Ctrl-D to fill in the function values corresponding to the first interval [2, 5]. For the interval [5, 13], we inserted the formula =B$17*(K7-B$5)^3+C$17*(K7-B$5)^2+D$17*(K7-B$5)+E$17 in cell L7, highlighted range L7:L14 and pressed Ctrl-D. Finally, for the interval [13, 15], we inserted the formula =B$18*(K15-B$6)^3+C$18*(K15-B$6)^2+D$18*(K15-B$6)+E$18 in cell L15, highlighted the range L15:L17 and pressed Ctrl-D.

Plot

We next highlighted range K4:L17 and selected Insert > Charts|Scatter using the Scatter with Smooth Lines option to obtain the blue curve on the right side of Figure 3.

Finally, we note that the original data values in range B4:C7 of Figure 1 were selected based on the function h(x) = ln(x+1) for x = 2, 5, 13, and 15. In fact, when we insert the graph of this function into Figure 3 (the red curve), we see that the spline function is a pretty good fit for the natural log function based only on interpolating between four points.

Real Statistics Support

Click here for a description of the Real Statistics function and data analysis tool that simplifies the process of creating a spline curve in Excel.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Chen, M-Q (2013) Cubic spline interpolation
The link is no longer available.

Jameson, A. (2019) Cubic splines
http://aero-comlab.stanford.edu/Papers/splines.pdf

Dunbar D. (2001) Cubic spline (Excel VBA implementation)
The link is no longer available.