In general, finding the roots of a polynomial requires the use of an iterative method (e.g. Newton’s method or Bairstow’s method). This is not necessary for linear and quadratic equations. It turns out that there is a non-iterative approach for finding the roots of a cubic polynomial. We describe this method here.
Methodology
The exact roots of a cubic polynomial a3x3 + a2x2 + a1x + a0 can be found using the following approach. Here, we assume that a3 ≠ 0; otherwise we have a quadratic polynomial. We can also assume that a0 ≠ 0; otherwise x = 0 is one root and the other roots are the roots of the quadratic polynomial a3x2 + a2x + a1.
Steps
Step 1: Since a3 ≠ 0, if we divide both sides of the equation a3x3 + a2x2 + a1x + a0 = 0 by a3, the left side of the equation will be a polynomial of form x3 + bx2 + cx + d with the same roots.
Step 2: Next, we make the substitution y = x + b/3, which results in the cubic equation
Note that the left side of the equation is a polynomial of form y3 + py + q, i.e. it doesn’t have a y2 term. If r is a root of this polynomial, then since x = y – b/3, it follows that r – b/3 is a root of the original cubic polynomial.
Step 3: We now make the substitution y = w + p/(3w), that transforms y3 + py + q = 0 into
We now make a further substitution u = w3
This equation can be solved using the quadratic formula
Now let Q = –q/2 and P = p/3, and so
Thus, there are 6 possible values for w, although it turns out that taking the plus sign or minus sign in front of the square root yields the same three solutions.
Step 4: If we knew that u were a real number then we could simply calculate w to be the (real) cube root of u, and then r = w – p/(3w) – b/3 would be one root of the cubic polynomial. Once we have found one root r of the cubic polynomial we can express the cubic polynomial as (x–r)f(x) where f(x) is a quadratic polynomial.
Observations
We can next find the two roots of f(x) using the quadratic formula, and these roots would be the remaining roots of the cubic polynomial. If you perform the (long division-like) factorization, assuming that r is a real number, you would see that f(x) = x2 + (b+r)x – d/r.
Since u could be an imaginary number, instead we will calculate all three cubic roots of u using the Real Statistics CRoots function as described in Polar Coordinates and Roots of a Complex Number. For each root w of u, w – p/(3w) – b/3 is a root of the original cubic polynomial. These calculations use complex number arithmetic even when the roots are real.
Observations
If Q2 + P3 < 0, then the cubic polynomial has three distinct real roots. If instead Q2 + P3 > 0, then the cubic polynomial has one real root and two imaginary roots. If Q2 + P3 = 0 then the cubic polynomial has one (real) triple root (namely –b/3) when P = 0, and one (real) double root and one (real) single root when P ≠ 0.
When the cubic polynomial has a triple root r, then the polynomial has the form (x–r)3 = x3 – rx2 + r2x – r3, In this case, the substitution in step 2 results in p = c – b2/3 = 3r2 – 3r2 = 0 and q = d + 2b3/27 – bc/3 = –r3 –2r3 + 3r3 = 0, and so the equation y3 + py + q = 0 becomes y3 = 0. Since y = x + b/3, this means that x + b/3 = 0, i.e. the triple root is –b/3.
Example
Example 1: Find the roots of the equation 2x3 – 6x2 +12x – 11
Step 1: This is equivalent to finding the roots of x3 – 3x2 +6x – 5.5
Step 2: Let y = x – 1. The polynomial then takes the form
Step 3: Thus, p = 3 and q = -1.5, and so P = 1 and Q = .75. Now
Thus, u = 2 or -.5. We’ll use u = 2.
Step 4: We next calculate all three cubic roots of u using the Real Statistics CROOTS function. For each root w, w – p/(3w) – b/3 is a root of the original cubic polynomial. These calculations use complex number arithmetic even when the roots are real.
A summary of the calculations is shown in Figure 1. The roots of the polynomial are 1.46621 and 0.76689 ± 1.77849.
Figure 1 – Finding roots of a cubic polynomial
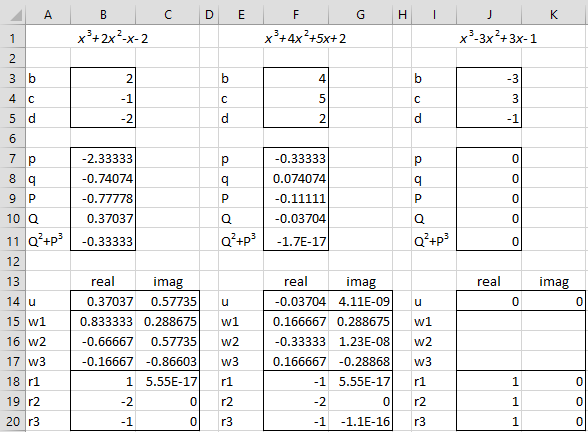
In Figure 2, we show the roots of some other representative cubic polynomials.
Figure 2 – Roots of a cubic polynomials
Worksheet Function
Real Statistics Function: The Real Statistics Resource Pack supplies the following function, where R1 is a column range containing the values b, c, d.
CubicRoots(R1) = a 3 × 2 array, in which each row contains one unique root of the polynomial x3 + bx2 + cx + d; each root is a 1 × 2 array where the first element represents the real part of the root and the second element represents the imaginary part.
Referring to Figure 1, the output from =CubicRoots(B3,B5) is the same as that shown in range B18:C20.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Links
References
Knaust, H. (1998) The cubic formula. S.O.S. MATHematics
No longer available online
Weisstein, E. W. (2018) Cubic formula, Mathworld, a Wolfram web resource
http://mathworld.wolfram.com/CubicFormula.html