Basic Concepts
A polynomial takes the form
for some non-negative integer n (called the degree of the polynomial) and some constants a0, …, an where an ≠ 0 (unless n = 0). The polynomial is linear if n = 1, quadratic if n = 2, etc.
A root of the polynomial is any value of x which solves the equation
Thus, 1 and -1 are the roots of the polynomial x2 – 1 since 12 – 1 = 0 and (-1)2 – 1 = 0.
By the Fundamental Theorem of Algebra, any nth degree polynomial has n roots. Unfortunately, not all of these roots need to be real; some can involve “imaginary” numbers such as , which is usually abbreviated by the letter i. For example, the equation x2 + 1 has the roots i and –i as can be seen by substituting either of these values for x in the equation x2 + 1 = 0.
Complex Roots
The class of all numbers which includes real numbers and imaginary numbers is called complex numbers
We now give three properties of complex numbers, which will help us avoid discussing imaginary numbers in any further detail:
- All complex numbers can be expressed in the form a + bi where a and b are real numbers; a is called the real part and b is called the imaginary part
- If a + bi is a root of an nth degree polynomial, then so is its conjugate a – bi
- If z = a + bi then the absolute value of z is defined by |z| =
Since a and b are real numbers, not involving , we only need to deal with real numbers.
Note that a complex number a + bi is real if b = 0. If a + bi is a real number then the definition of absolute value given above agrees with the ordinary definition since |a| =
Quadratic Polynomials
The roots of a quadratic polynomial a2x2 + a1x + a0 are given by the quadratic formula, namely
If the value inside the square root symbol is negative, then both roots are imaginary, while if the value inside the square root symbol is non-negative then both roots are real.
Factorization
By the Fundamental Theorem of Algebra, not only does every nth degree polynomial have n roots, but we can use these roots as a factorization of the polynomial. More specifically, if r1, r2, …, rn are these roots then we can factor the polynomial as follows
![]()
Here, we include multiple roots, i.e. roots that are repeated more than one time in the factorization. E.g. the quadratic polynomial x2 + 2x + 1 = (x+1)(x+1), and so -1 is a root two times.
In the polynomial
if a0 = 0, then it is easy to see that zero is a root, and in fact, the polynomial can be factored as
and so the n roots are zero plus the roots of the n–1 degree polynomial anxn-1 + an-1xn-2 +…+ a1. In fact, if a1 = 0, then zero is a double root and the polynomial can be factored as
If we factor out all the zero roots of the polynomial, we can assume that the constant coefficient of the polynomial that remains is non-zero.
Initial Coefficient
If all we care about are the roots of the polynomial, we can assume that the first coefficient is 1 since
has the same roots as our original polynomial and an/an = 1. Thus, where we are only concerned with roots, we can consider our original polynomial to take the form
Cubic Polynomials
In general, finding the roots of a polynomial requires the use of an iterative method (e.g. Newton’s method or Bairstow’s method, as described below). This is not necessary for linear and quadratic equations, as we have seen above. It turns out that there is a non-iterative approach for finding the roots of a cubic polynomial. See Cubic Polynomials.
Real Statistics Approach
The following Real Statistics function implements Bairstow’s Method to find all the roots of a polynomial.
Real Statistics Function: The Real Statistics Resource Pack supplies the following array function where R1 is an n+1 × 1 range containing the coefficients of the polynomial where a0 is in the first position and an is in the last position.
ROOTS(R1): returns an n × 2 range where each row contains one root, and where the first column consists of the real part of the roots and the second column consists of the imaginary part of the roots
Note that the value in the last position of R1 (corresponding to an) does not have to be one, but it cannot be zero. The value in any other position of R1 can be zero.
Simple example
Example 1: Find the roots of
The results are shown in Figure 1
Figure 1 – Finding the roots of a polynomial
Here range D6:E9 contains the array formula =ROOTS(B6:B10).
As you can see, the four roots are 2i, -2i, -5 and 3.
Repeated roots example
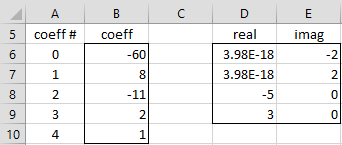
Example 2: Find the roots of
The results are shown in Figure 2
Figure 2 – Finding the roots of a polynomial
This time the roots are 0, 1, -1 (twice).
Additional arguments
The ROOTS function actually takes a number of optional parameters
ROOTS(R1, prec, iter, r, s)
prec = the precision of the result, i.e. how close to zero is acceptable. This value defaults to 0.00000001.
iter = the maximum number of iterations performed when performing Bairstow’s Method. The default is 50.
r, s = the initial seed values when using Bairstow’s Method. These default to zero.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Links
References
Kumar, R. (2002) Numerical analysis
https://archive.nptel.ac.in/content/storage2/courses/122104019/numerical-analysis/Rathish-kumar/ratish-1/f3node9.html
Wikipedia (2016) Polynomial root finding
https://en.wikipedia.org/wiki/Polynomial_root-finding
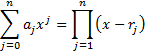
Can you send me Solver Password.
Thanks.
Hello Srecko,
Sorry, but I don’t have the Solver password.
Charles
Dear Dr Zaoinitz, I hope all is ok. Dr I think that there is an error when you look for solutions or roots of a cuadratic polynomial, allway you have de same solution in anyone cuadritic polynomial.
Thank you very much
Hello Gerardo,
I am doing well. I hope this is true for you also.
The example given in a quadratic polynomial. The solution consists of 4 distinct roots.
If I change the a_0 coefficient from -60 to 1, I get a completely different solution consisting of 4 distinct real values.
Not clear what you mean by “the same solution”.
Charles
The factorization of a polynomial you describe is missing the factor “a sub n” multiplying the product of (x-ri)
Hi Enrico,
Thanks for bringing this issue to my attention, but I can’t find any reference to (x-ri) at all (including where i is a subscript). I do have a reference to (x-rn) in the first formula in the Factorization section. Is this what you are referring to? This seems ok.
Charles