On this webpage, we describe Real Statistics worksheet functions that implement the root-finding methods described at Roots of a Continuous Function.
These functions take a lambda function parameter, which is a parameter that is a function. These are described in Real Statistics Lambda Capabilities and Lambda Functions using Cell Formulas.
Worksheet Functions
Real Statistics Functions: The Real Statistics Resource Pack provides the following worksheet functions.
BISECTION(R1, lower, upper, iter, prec, Rx) = a root of f(x) in the interval (lower, upper) based on the bisection method.
SECANT(R1, x0, x1, iter, prec, Rx) = a root of f(x) based on the secant method and two initial points x = x0 and x = x1.
BRENT(R1, lower, upper, iter, prec, Rx) = a root of f(x) in the interval (lower, upper) based on Brent’s method.
NEWTON(R1, guess, iter, prec, incr, Rx) = a root of f(x) based on Newton’s method using the specified initial guess.
R1 is a cell that contains a formula that represents the function f(x) and the address of cell Rx references the variable x in R1. If Rx is omitted, then it defaults to the first cell referenced in R1.
iter (default 100) = the maximum number of iterations. The algorithm will terminate prior to iter iterations if the error is less than some value based on prec (default .0000001).
For the NEWTON function, guess is the initial guess for the root. Since this approach uses the Real Statistics function DERIV to estimate the derivative of the function f(x), the incr parameter used by DERIV needs to be specified (default .000001); See Numerical Differentiation.
If the formula in R1 doesn’t contain a cell address, then a #N/A error value is returned. A #NA error value is also returned for BISECTION or BRENT when the interval (lower, upper) doesn’t bracket a root. If a #NUM is returned then the algorithm doesn’t converge in less than iter iterations. If some step in any of these processes requires division by zero, then a #VALUE! error will be returned.
Finding Multiple Roots
Since there can be more than one root of a function in an interval, we can also use the following array function to attempt to find all the roots.
NROOTS(R1, lower, upper, nguess, iter, prec, incr, Rx): returns a column array with all the roots of f(x) in the interval (lower, upper) based on Newton’s method.
This function finds the roots based on nguess (default 50) equally spaced guesses initial guesses chosen randomly from the interval (lower, upper). There is no guarantee that all the roots will be found, but for nguess chosen large enough, usually, you should be able to obtain all the roots (up to a maximum of 100 roots).
If nguess < 0 then the process is the same except that –nguess initial guesses are chosen randomly from the interval (lower, upper).
Example
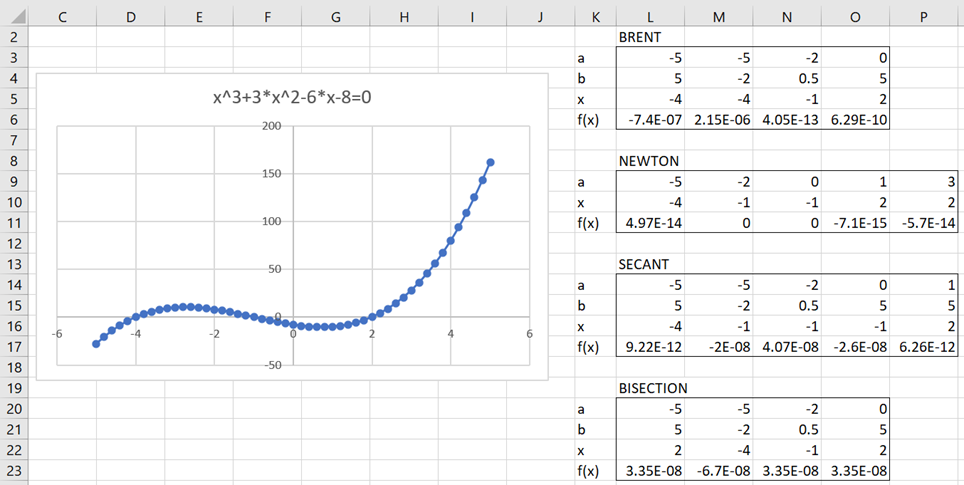
Example 1: Find the roots of the function f(x) = x3 + 3x2 – 6x – 8 in the interval (-5. 5) using the various methods described above.
The results are shown in Figure 1 where (a,b) represent different values for x. Note that different roots x are found depending on the values of a and b. Also, note that the different methods may determine different roots.
Figure 1 – Roots of a function
For example, the formula =BRENT(B3,L3,L4) in cell L5 finds the root -4. The same root is found when a = -5 and b = -2. Here cell B3 contains the formula =A3^3+3*A3^2-6*A3-8.
The formula =NEWTON(B3,O9) in cell O11 finds the root 2 based on the initial guess of 1.
The array formula =NROOTS(B3,-5,5) (not shown in Figure 1) returns a column range with the values 2, -1, and -4.
Finally, note that these worksheet functions can be used with any continuous function f(x), not just polynomials.
Repeated Roots Example
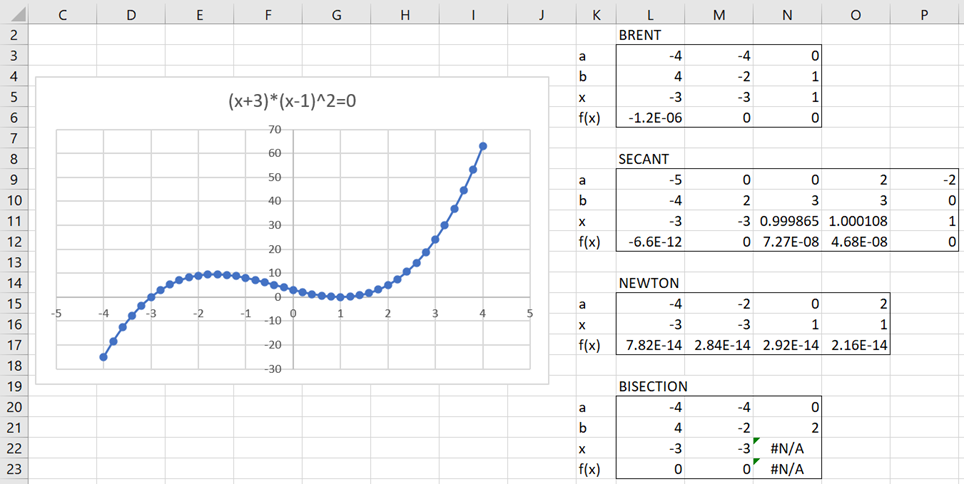
Example 2: Find the roots of the function f(x) = (x+3)(x-1)2 in the interval (-4. 4).
The results are shown in Figure 2.
Figure 2 – Roots for a function with a local minimum
This time there are two roots x = -3 and x = 1 (repeated). The Bisection and Brent’s method can’t detect this second root since there is no interval that brackets the root where the function on one side is positive and the other side is negative (except when the root itself is one of the endpoints of the interval).
Newton’s method finds both roots as does the secant method, although the values in cells N11, O11, and P11 all refer to the same root.
Final Observation
For a constant function, say f(x) = 3, for any of the above functions, the first argument must be a cell containing a formula such as =A1*0+3. Since a reference to x must be used, we can’t simply specify the formula as =3.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Links
↑ Roots of a continuous function
References
Wikipedia (2021) Bisection method
https://en.wikipedia.org/wiki/Bisection_method
Wikipedia (2021) Secant method
https://en.wikipedia.org/wiki/Secant_method
Wikipedia (2021) Brent’s method
https://en.wikipedia.org/wiki/Brent%27s_method
Wikipedia (2021) Newton’s method
https://en.wikipedia.org/wiki/Newton%27s_method