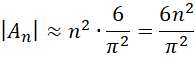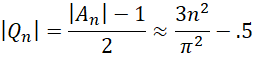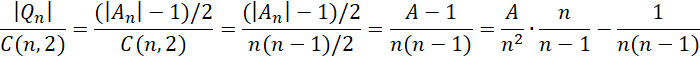Rational Numbers in Qn| Real Statistics Using Excel

Objective

A rational number is a quotient of two integers. For our purposes, we will restrict ourselves to positive integers and rational numbers in the interval (0, 1).

For any positive integer n, our goal is to obtain a list of all the unique rational numbers h/k in the interval (0,1) where h < k ≤ n. We call the set of such rational numbers Q_n. We also want to know the number of elements in Q_n, denoted |Q_n|.

E.g. if n = 5, there are 9 qualifying rational numbers, namely 1/2, 1/3, 1/4, 1/5, 2/3, 2/5, 3/4, 3/5, and 4/5. There are a maximum of C(n,2) pairs of such integers. When n = 5, C(5,2) = 10, but 2/4 is a duplicate entry since ½ is already on the list.

As you can see, the number of such rational numbers is related to the number of pairs of coprime integers, namely

Q_n = {h/k : 0 < h < k ≤ n and gcd(h, k) = 1}

In fact, if you don’t take the order of the two numbers into account, the number of such rational numbers is one less than the number of coprimes since 1 is coprime with itself but 1/1 is not in the interval (0,1).

Worksheet Functions

Real Statistics Functions: The Real Statistics Resource Pack provides the following worksheet functions.

FRACS(n): returns an array with three columns. Column 1 contains the values in Q_n in decimal form, and the other two columns contain the corresponding h and k values for an h/k in Q_n

NFRAC(n) = the number of unique elements in Q_n

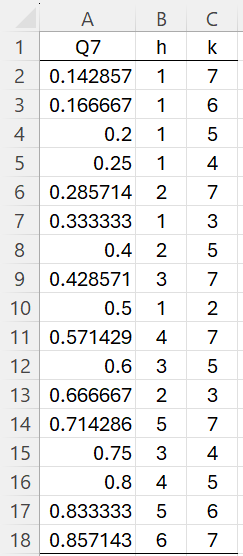
Example 1: What are the elements in Q₇?

Using the formula =FRACS(7), we obtain the output shown in A2:C18 of Figure 1.

Figure 1 – Q₇

We see that the first element in Figure 1 is 1/7 = .142857.

We also see that |Q₇| = 17. You can get the same result using the formula =NFRAC(7).

Note that there are C(7,2) = 21 distinct pairs of integers between 1 and 7, and so there are a maximum of 21 elements in Q₇. The four fractions 2/4, 2/6, 4/6, and 3/6 are already in the list of elements in Q₇, namely as 1/2, 1/3, 2/3, and 1/2, bringing the total down to 21-4 = 17 elements.