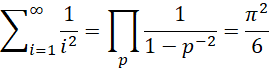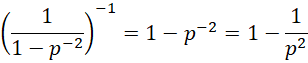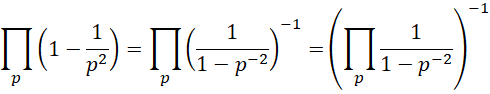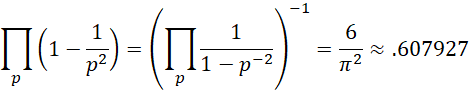Coprime Numbers | Real Statistics Using Excel

Two integers h and k are coprime if they don’t have a common factor > 1. That is the great common divisor of h and k, gcd(h,k), is one.

For any integer n, the number of rational numbers h/k where 0 < h < k <= n is equal to the number of pairs of distinct positive integers <= n that are coprime.

Worksheet Function

Excel Function: Excel provides the following worksheet function.

GCD(h,k) = the greatest common divisor of integers h and k

E.g. the gcd of 60 and 42 is 6, and so GCD(42, 60) = 6. This is so since 60 = 3*4*5 and 42 = 3*2*7. The gcd is therefore 2*3 = 6.

Actually, GCD can also output the gcd of more than two integers. Also, if R1 is an array or cell range, then GCD(R1) = the gcd of all the elements in R1.

Recall too that the least common multiplier of h and k, denoted lcm(h,k), is equal to hk/gcd(h,k). This can be calculated in Excel by the formula h*k/GCD(h,k).

Number of Coprimes

Property 1 (Euler)

Here the product is taken over all prime numbers

Property 2: The probability that two positive integers selected at random are coprime is 6/π².

Proof: For any prime number p the probability that any positive integer h selected at random is divisible by p is 1/p (i.e. all the multiples of p).

Thus, the probability that two positive integers h and k selected at random are both divisible by p is 1/p². Hence, the probability that both are not divisible by p is 1 – 1/p².

Note that