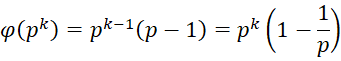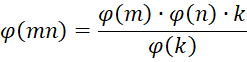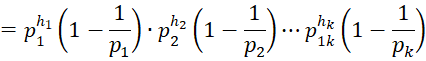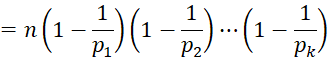Fraction to Decimal – Details

Euler’s Function

Euler’s function φ(n) = # of integers h such that 1 ≤ h < n and gcd(h, n) = 1 (i.e. h/n can’t be reduced).

Property 1: If p is a prime and k > 0 then

Property 2: If gcd(m,n) = k, then

Thus, if If gcd(m,n) = 1, then

Property 3: If n = 2^km where k > 0 and m is odd then

Property 4: If the prime factorization of n is

then

Property 5: φ(n) is even for all n > 2. In fact, if n has k distinct odd prime factors, then 2^k | φ(n).

Worksheet Function

Real Statistics Function: The Real Statistics Resource Pack provides the following worksheet function.

EULER(n) = φ(n)

Repeating period

As described in Converting a Fraction to a Decimal, the decimal form of a fraction is either terminating or repeating. We define ρ(n) = the length of the repeating portion of the fraction 1/n. If 1/n is terminating then ρ(n) = 0. Recall that the length of the repeating portion of a fraction m/n where gcd(m, n) = 1 is also ρ(n).

Property 6: If n = 2^h5^km where m is not divisible by 2 or 5. then ρ(n) = ρ(m).

Property 7: If n is not divisible by 2 or 5, then ρ(n) | φ(n).

In particular, if p is a prime number not equal to 2 or 5 and k > 0, then ρ(p^k) | φ(p^k).

Property 8: If m and n are not divisible by 2 or 5 and gcd(m,n) = 1, then ρ(mn) = lcm(ρ(m),ρ(n)).

Examples

First note that

By Property 8

ρ(189) = ρ(7⋅27) = lcm(ρ(7),ρ(27)) = lcm(6,3) = 6

ρ(7749) = ρ(7⋅27⋅41) = lcm(ρ(7),ρ(27),ρ(41)) = lcm(6,3,5) = 30

By Properties 1 and 7

ρ(7⁶) | φ(7⁶) = 7⁵ ⋅ 6

Thus, the possible values for ρ(7⁶) are

7^h          7^h⋅ 2          7^h⋅ 3          7^h⋅ 6

for h = 0, 1, 2, 3, 4, 5. Hence there are 6 ⋅ 4 = 24 possibilities for the value of ρ(7⁶). 

Using the prime factorization

If the prime factorization of n is

and m_i = φ(p_i^hi) where none of the p_i are 2 or 5, then by Property 8

ρ(n) = lcm(m₁, m₂, …, m_k) = n/gcd(m₁, m₂, …, m_k)

The values of the m_i can be found using Property 7.

In fact, by Property 6, if the prime factorization of n is as above, then ρ(2^h5^ln) = ρ(n) = lcm(m₁, m₂, …, m_k).

We can use Real Statistics’ FRAC_REP(m) to calculate ρ(n) for any positive integer n (see Converting a Fraction to a Decimal).

Fixed period

As described in Converting a Fraction to a Decimal, the fixed portion of the decimal representation of a fraction is the part that precedes the repeating part. Define τ(n) = the length of this fixed part.

Since 1/4 = .25, τ(4) = 2. Also, τ(3) = 0 since 1/3 = .333… and τ(6) = 1 since 1/6 = .1666…

Property 9: If m = 2^h5^k, then τ(m) = max(h, k).

Property 10: If m = 2^h5^k and n is not divisible by 2 or 5, then τ(mn) = τ(m) and ρ(mn) = ρ(n).

We can use Real Statistics’ FRAC_FIXED(m) to calculate τ(m) for any positive integer m (see Converting a Fraction to a Decimal).

References

Wikipedia (2023) Repeating decimal
https://en.wikipedia.org/wiki/Repeating_decimal

Lyons, C. (2016) The secret life of 1/n: A journey far beyond the decimal point. Mathematical Enthusiast
https://scholarworks.umt.edu/tme/vol13/iss3/3

Wikipedia (2023) Euler’s totient function
https://en.wikipedia.org/wiki/Euler%27s_totient_function