On this web page, we show how to convert a fraction h/k to decimal form.
Long Division
The basic approach for converting a fraction h/k to decimal form is by using long divisions. E.g. the fraction 3/44 can be converted to the decimal .06818181… as shown in Figure 1.
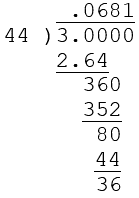
Figure 1 – Long division
We see that the 36 difference in the calculation is repeated, which results in the repeating 81.
Repeating and Terminating Forms
As described in Converting a Decimal to a Fraction, rational numbers when expressed as a decimal number can take one of two forms: (1) terminating, i.e. they have a finite number of decimal places, or (2) repeating, i.e. the decimal portion repeats endlessly. E.g. 1/2 = .5 and 3/8 = .375 are terminating, while 1/3 = .333… , 2/11 = .181818…, and 2/15 = .1333… are repeating.
Note that which form the fraction m/n takes only depends on the denominator n.
If n > 1 is of the form 2h5k where h and/or k is a non-negative integer, then m/n is terminating; otherwise, it is repeating.
Worksheet Functions
Excel supports decimals with 15 significant digits. Unfortunately, for many fractions 1/n even with a small value of n, the repeating part of the decimal exceeds 15 digits. E.g. the repeating part of 1/19 requires 18 digits and the repeating part of 1/23 requires 22 digits. Thus, we need to represent such decimal expressions as text instead of a number.
Real Statistics Functions: The Real Statistics Resource Pack provides the following worksheet functions.
FRAC2DEC(n, m) = a text representation of m/n as a decimal where 1 ≤ m < n
FRAC_REP(n, m) = the number of repeating digits in the decimal representation of m/n
FRAC_FIXED(n, m) = the number of fixed digits in the decimal representation of m/n
If m is omitted it defaults to 1.
For example
- FRAC2DEC(4, 3) = “0.75”
- FRAC2DEC(6) = “0.1 6…”
- FRAC2DEC(19) = “0. 052631578947368421…”.
Fractions that have a repeating part terminate in “…”. The repeating part is preceded by a space. Thus, 1/6 is expressed by “0.1 6…” where .1 is the fixed part and 6 is the repeating part. 3/4 doesn’t have a repeating part and so is expressed as “0.75” (no space and no terminating …).
Also
- FRAC_REP(4, 3) = 0, FRAC_REP(6) = 1, FRAC_REP(19) = 22
- FRAC_FIXED(4, 3) = 2, FRAC_FIXED(6) = 1, FRAC_FIXED(19) = 0
More information
Click here for more information about how to calculate the length of the fixed and repeated parts of a decimal representation of a fraction.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Wikipedia (2023) Repeating decimal
https://en.wikipedia.org/wiki/Repeating_decimal
Lyons, C. (2016) The secret life of 1/n: A journey far beyond the decimal point. Mathematical Enthusiast
https://scholarworks.umt.edu/tme/vol13/iss3/3
Pierce, R. (2023) Long division
https://www.mathsisfun.com/long_division.html