Polar Coordinates and Roots of a Complex Number

Basic Concepts

Complex numbers (c, d) (in rectangular format) can be converted to polar format (r, θ) using the formulas r = and θ = arctan(d/c). Note that r = |z| (the absolute value) and we use the notation arg r for θ. In Excel, this can be expressed by r = SQRT(c^2+ d^2) and θ = ATAN2(c, d). Note that there are an infinite number of equivalent polar formats; in fact, for any integer k, (c, d) can also be represented by the polar format (r, θ+kπ), where π = Pi().

The inverse transformation, converting polar format into rectangular form is accomplished via the formulas c = rcosθ and d = rsinθ which in Excel is c = r*COS(θ) and d = r*SIN(θ). It thus follows that (c, d) = rcosθ + i rsinθ, which it turns out is equivalent to re^θi.

Because of the properties of the exponential function re^θi (or similar properties for rcosθ + rsinθ·i), some of the operations described in Complex Number Operations are easier to perform using polar notation. E.g. if z is (r, θ) in polar format, then zⁿ = (re^θi)ⁿ = rⁿe^nθi, which is (rⁿ, nθ), which is (rⁿ cos(nθ), rⁿ sin(nθ)) in rectangular format, or equivalently (|z|ⁿ cos(n·argz), |z|ⁿ sin(n·argz)).

We can find the n^th root of a complex number in the same way, namely (r^1/n, θ/n). Since r and θ are real numbers, these values can be obtained easily in Excel to find one n^th root, but by the Fundamental Theorem of Algebra (see Roots of a Polynomial), there are n such roots. These can be found by recalling that (r, θ) is equivalent (r, θ+kπ) for all integers k. Thus, (r^1/n, (θ+kπ)/n) is also an n^th root of (r, θ). It is sufficient to use values of k = 0, 1, …, n-1 to get all n unique roots.

Worksheet Functions

Real Statistics Functions: The Real Statistics Resource Pack supplies the following functions, where z is a 1 × 2 range which represents a complex number in rectangular format and zz is a 1 × 2 range which represents a complex number in polar format.

CPolar(z) = 1 × 2 range with z in polar format

CRect(zz) = 1 × 2 range with zz in rectangular format

CRoots(z, n) = n × 2 range in which each row represents one of the n unique n^th roots of z

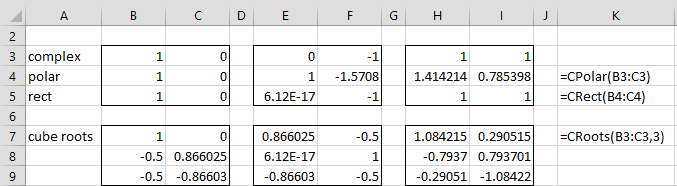
Figure 1 shows the complex numbers 1, –i,  and 1 + i, and shows how to convert them to polar format, and then back to rectangular format. It also shows the cube roots of each of these complex numbers. E.g. the cube roots of 1 are 1, -0.5+0.86603i, and -0.5-0.86603i. Note that 0.86603 is √3/2, and so the two imaginary roots are (-1±√3)/2.

Figure 1 – Polar format and cube roots

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Wikipedia (2018) Polar coordinate system
https://en.wikipedia.org/wiki/Polar_coordinate_system#:~:text=In%20mathematics%2C%20the%20polar%20coordinate,angle%20from%20a%20reference%20direction.

Abramson, J. (2023) Polar form of complex numbers. OpenStax
https://math.libretexts.org/Bookshelves/Precalculus/Precalculus_1e_(OpenStax)/08%3A_Further_Applications_of_Trigonometry/8.05%3A_Polar_Form_of_Complex_Numbers