Objective
On this webpage, we show how to calculate double integrals of the following form using numerical methods.
where
Numerical Estimation
In particular, we can use the techniques described in Numerical Integration, to calculate g(y) for any value of y. Then by Simpson’s rule for the outer integral, we see that
where the interval [c, d] is divided into n equal subintervals. Using the mappings described in Numerical Integration, we can also calculate the double integral where c = -∞ or d = ∞, or both.
We can also handle the situation where a and/or b is replaced by a function of y. In this case
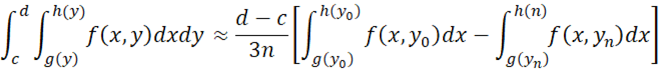
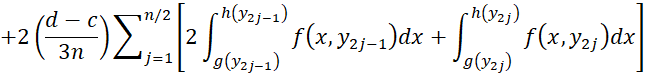
Worksheet Function
Real Statistics Function: The Real Statistics Resource Pack provides the following function.
INTEGRAL2(R1, lox, upx, loy, upy, iterx, itery, Rx, Ry) = ∫∫ f(x,y)dxdy between x = lox and upx, and between y = loy and upy using Simpson’s rule.
R1 is the address of a cell that contains a formula that represents a function f(x, y) in two variables. Rx and Ry contain optional cell addresses for x and y. If omitted these addresses default to the first address and, if necessary, the second address in the formula in R1. This provides lambda functionality for functions in two variables.
loy and upy contain the values of the outer integral limits. These are numeric values, although if loy is omitted then -infinity is used, while if upy is omitted then +infinity is used.
lox and upx contain the values of the inner integral limits. These can take either numeric values or can define a function g(y). In the latter case, lox or upx contains the address of the formula that defines g(y) using Ry if this argument is present. lox and upx cannot be omitted.
iterx = the number of x-axis subintervals and itery = the number of y-axis subintervals. Both of these default to 400.
Cautions
Note that the formula in cell R1 can’t refer to any cells that in turn refer to cell Rx (or the first cell referenced in R1 if Rx is omitted) or Ry (or the second cell referenced in R1 if Ry is omitted).
If a #VALUE! error is returned it is quite possible that an overflow error has occurred. This can mean that the integral does not converge to a finite value. This can also occur when a large positive or negative value is returned, especially when the value of iterx or itery is set to a low number so that overflow hasn’t yet occurred.
R1 and optionally lox and upx can be replaced by a LAMB or the string version of the lambda function, as described in Lambda Functions using Cell Formulas.
Examples
Click here for examples of how to use the INTEGRAL2 worksheet function.
Links
Reference
Mahaffy, J. (2010) Numerical integration and differentiation – multiple integrals; improper integrals
https://jmahaffy.sdsu.edu/courses/s10/math541/lectures/pdf/week09/lecture.pdf