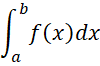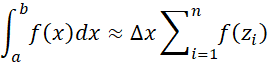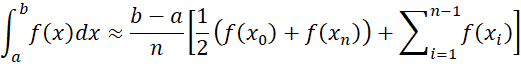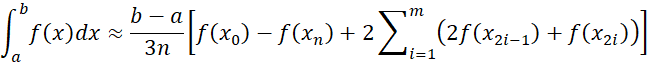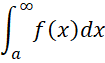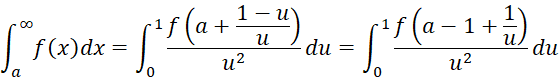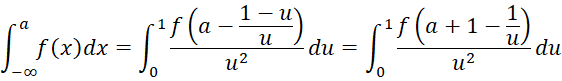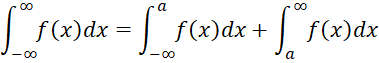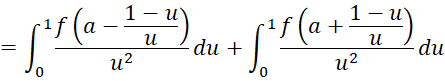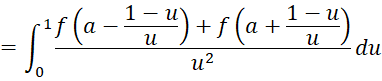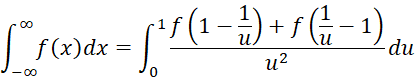Objective
Our goal is to estimate the value of a definite integral of the form
We divide the interval [a, b] into n equally sized subintervals where a = x0 < x1 < ⋅⋅⋅ < xn = b and where xi+1 = xi + Δx and Δx = (b–a)/n. Thus, xi = a + Δx⋅i.
Midpoint Rule
A commonly used way of estimating the definite interval is as follows:
Here, we assume
Thus
The maximum error using this approach is
where
Trapezoid Rule
Another commonly used way of estimating the definite interval is as follows:
The maximum error for the trapezoid rule is
Simpson’s Rule
The final estimation approach that we will consider is
Here, n is even with n = 2m. The maximum error for Simpson’s rule is
Non-finite limits
The above approaches don’t work when the integral limits a and b are not finite, i.e. a = -∞ and/or b = ∞. One approach for dealing with such cases is to use a transformation. For example, to deal with
when the lower limit a is finite but the upper limit is not, is to use the transformation
Thus
Also, if u = 0 then x = ∞. If u = 1 then x = a. This means that
When the lower limit is -∞, we can use the following transformation
Thus
When both limits are non-finite, we see that for any a
If we choose a = 0, we get
Real Statistics Function
The various estimation techniques described above have been implemented in the Real Statistics Resource Pack via the INTEGRAL function. Click here for more information about this function as well as numerous examples of how to use it in Excel.
Double Integration
Click here for information about how to perform double integration.
References
Wikipedia (2021) Numerical integration
https://en.wikipedia.org/wiki/Numerical_integration
Bourne, M. (2021) Simpson’s Rule. Interactive Mathematics
https://www.intmath.com/integration/6-simpsons-rule.php
Wikipedia (2021) Riemann sum
https://en.wikipedia.org/wiki/Riemann_sum