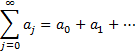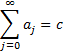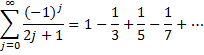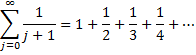Infinite Series

Convergence of an infinite series

An infinite series takes the form

image056c

Letimage057c

be the nth partial sum of this series. The infinite series converges (i.e. takes a finite value c) provided

image058c

In this case, we say thatimage059c

Our goal is to determine when an infinite series converges.

Note that we can change the initial value of the sum without changing whether the series converges or not. E.g. if \sum\limits_{j=0}^\infty a_j = c, then \sum\limits_{j=1}^\infty a_j converges to the value c – a0. Similarly, if \sum\limits_{j=2}^\infty a_j = d, then \sum\limits_{j=1}^\infty a_j converges to the value d + a0 + a1.

Alternating Series Test

Property 1: If {a0, a1, …} is an alternating series (i.e. the signs of the terms alternate between plus and minus) with |a0| ≥ |a1| ≥ |a2| ≥ … and \lim_{n\to\infty} {|a_n|}, then \sum\limits_{j=0}^\infty a_j converges

Proof: Let sn = \sum\limits_{j=0}^n a_j be the nth partial sum. Our goal is to show that \lim_{n\to\infty} {s_n} = 0.

Suppose that a0 ≥ 0 (the proof is similar if a0 < 0 since a1 ≥ 0, and so we can perform the same analysis starting from a1 instead of a0). Define bn = |an| for all n. Thus, the original series is {b0, –b1, b2, –b3, …} where bn ≥ 0 for all n.

Since we have assumed that {b0, b1, b2, b3, …} is a decreasing series, it follows that for any n

image066c

It then follows that for any odd value of n

image067c

which shows that {s1, s3, s5, …} is an increasing series.

Now for any odd value of n

image068c
image069c

Note that all the terms in parentheses are positive as is bn, and so sn ≤ b0 for all odd values of n. Since {s1, s3, s5, …} is an increasing series that is bounded above, it follows that the series converges to some finite value s.

Note too that if n > 0 is even, then sn = sn-1 + bn. Since the sn-1 values converge to s (since n–1 is odd) and the bn values converge to 0 (by assumption), it follows that the sn for odd values of n converge to s+0 = s. Thus, all the values of sn converge to s.

Alternating Series Example

By Property 1, the alternating series

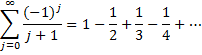image070cconverges. It turns out that it converges to ln 2. Also by Property 1, the series

image071c

converges. It turns out that this series converges to π/4.

Harmonic Series

The harmonic series

image072c

diverges. To see this, note that the infinite sequence of partial sums {s0, s1, s2, …} is an increasing series that is unbounded and therefore diverges. We see that it is unbounded since

image073c

image074c

image075c

Reference

Wikipedia (2016) Series (mathematics)
https://en.wikipedia.org/wiki/Series_(mathematics)

Leave a Comment