Prim Algorithm
We show how to construct a minimum spanning tree (MST) for a connected graph using the Prim algorithm.
Whereas the Kruskal algorithm sequences through the edges to find the MST, the Prim algorithm sequences through the nodes 1, 2, …, n-1. This algorithm uses the following three functions: p (parent), k (key), and q (set to TRUE if the node has not yet been evaluated).
Step 0: Initialize these functions by p(i) = 0, k(i) = ∞, q(i) = TRUE for each node i, except set k(1) = 0.
Steps 1 through n-1: Find the node j for which k(j) is smallest among the nodes that have not yet been evaluated, i.e. for which q(j) = TRUE. In the case of ties, we can choose the first node for which k(j) is the smallest. Note that in step 1, j = 1.
We set q(j) = FALSE and then evaluate any edge in the graph that is connected to j, i.e. edges of the form (i, j) or (j, i). For such an edge, if q(i) = TRUE and k(i) is greater than the weight of this edge, then we set k(i) to the weight of this edge and p(i) = j. As a result, the key and parent values for one or more nodes may be adjusted; it is also possible that the value for none of the nodes is adjusted.
After we have carried out all the steps, all the edges of the form (i, p(i)) constitute the MST.
Examples
Example 1: Repeat Example 1 of Kruskal Algorithm using the Prim algorithm.
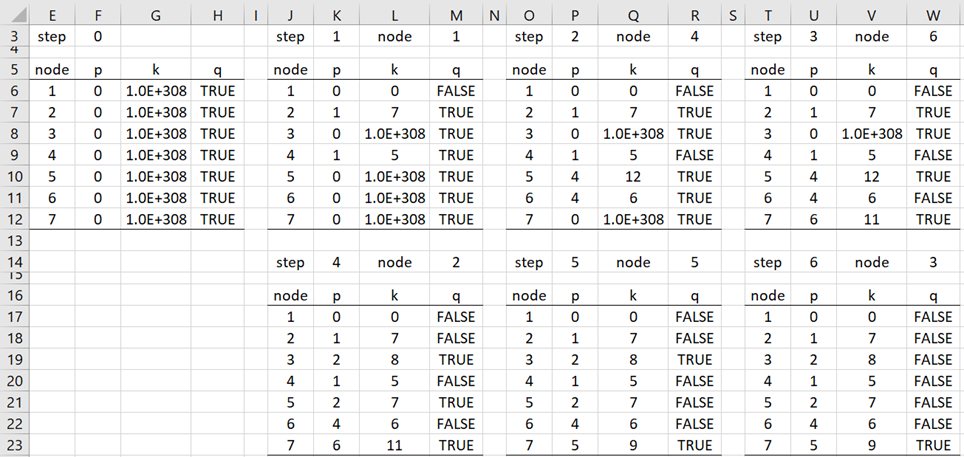
We show the analysis in Figure 1. Here, we represent infinity by a large positive number, namely 1.0E+308.
Figure 1 – Prim algorithm
In the final step, we see that p(2) = 1, p(3) = 2, p(4) = 1, etc. This means that the edges (1,2), (3,2), (4,1), etc. are in the MST. It turns out that these are the same edges that are generated from the Kruskal algorithm.
Worksheet Functions
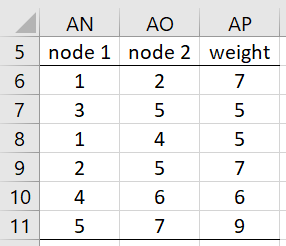
Real Statistics Function: The Real Statistics Resource Pack contains the following array function where R1 is an array with three columns where the first two columns contain the node numbers of the graph in ascending order and the third column contains the weights for the edge defined in each row.
MSTPrim(R1, brief): returns an array with the rows from R1 that constitute an MST for R1 using the Prim algorithm assuming that brief = FALSE (default).
When brief = TRUE, then the output is the same as when brief = FALSE except that the third column is not included.
For Example 1, the array formula =MSTPrim(A4:C14) produces the output shown in Figure 2.
Figure 8 – MSTPrim results
This is the same as that shown in Figure 5 of Kruskal Algorithm, except that the order of the rows is different.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Reference
GeeksforGeeks (2020) Prim’s minimum spanning tree (MST), Greedy algorithm Algo-5
https://www.geeksforgeeks.org/prims-minimum-spanning-tree-mst-greedy-algo-5/