Basic Concepts
A graph G = (N, E) consists of a set of nodes N (aka vertices) and edges E (aka links) which connect two nodes to each other. For our purposes, we will assume that N and E are finite and that the edges are undirected, and so can be defined uniquely as a pair of nodes (n1, n2) where n1 ≠ n2. We will also assume that all edges have a weight, which is a non-negative numeric value, and so if (n1, n2) is an edge in the graph under consideration, there is a function w(n1, n2) that defines the weight of this edge.
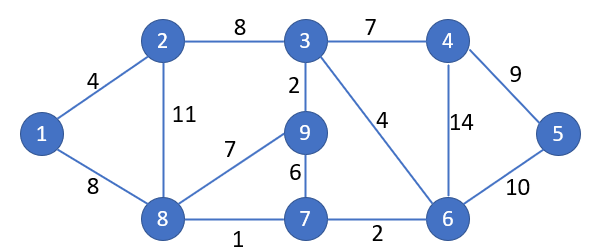
In what follows, we will label nodes by 1, 2, …, n where n is the number of nodes in N. We can describe a graph by a network diagram as shown in Figure 1.
Figure 1 – Network Diagram
Graph representation in Excel
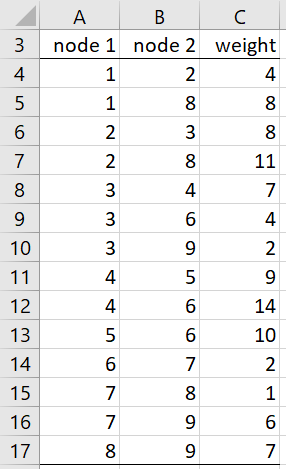
We will represent this same graph in Excel as shown in Figure 2.
Figure 2 – Excel representation of a graph
Each row in range A4:C17 represents one of the 14 edges in the graph. Each row specifies the two nodes being connected as well as the weight of the edge.
Path
A path between nodes i and j consists of a series of nodes n1, n2, …, nk such that i = n1, j = nk and (n1,n2), (n2,n3), …, (nk-1,nk) are edges in the graph. A graph is connected if there is a path between any two nodes in the graph. A graph is fully-connected if every node is connected (via an edge) to every other node.
A cycle is a path between and node and itself. A tree is a graph with no cycles. A graph G′ = (N′, E′) is a subgraph of G = (N, E) if N′ is a subset of N and E′ is a subset of E. A subgraph G′ of G spans graph G if N′ = N.
Spanning Tree
A spanning tree G′ of graph G is a subgraph of G that is a tree that spans G. The total edge weight of a graph is the sum of the weights of all the edges in the graph. G′ is a minimum spanning tree (MST) of G if it is a spanning tree of G whose total edge weight is smallest, i.e. there is no other spanning tree with a smaller total edge weight.
Note that any connected graph has a minimum spanning tree. This minimum spanning tree does not necessarily have to be unique. An unconnected graph has a minimum spanning forest.
In the following, we describe two algorithms for creating a minimum spanning tree of a connected graph. We will also show how to construct a minimum spanning tree for the graph G = (N, E) where N = a set of r-tuples (i.e. points in r-space) and E consists of all the lines connecting any two of the r-tuples in N.
Topics
- Kruskal Algorithm for MST
- Prim Algorithm for MST
- MST for r-tuples
- Creating a network diagram using Excel charting capabilities
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Links
Reference
Cormen, T. H., Leiserson, C. E., Rivest, R. L. (1992) Introduction to algorithms. MIT Press.
https://mitpress.mit.edu/books/introduction-algorithms-third-edition
Wilson, R. J. (1996) Introduction to graph theory. 4th ed. Prentice Hall
https://webhomes.maths.ed.ac.uk/~v1ranick/papers/wilsongraph.pdf