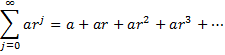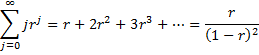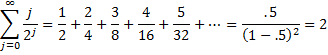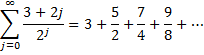Geometric Series

Basic Concepts

A geometric series is an infinite series which takes the form

for some constants a and r.

Property 1: If |r| < 1 then the geometric series converges to $\frac{a}{1-r}$

Proof: First we note that $\sum\limits_{j=0}^\infty {ar^j}$ = a $\sum\limits_{j=0}^\infty {r^j}$ , and so the series converges if and only if $\sum\limits_{j=0}^\infty {r^j}$ converges, and if $\sum\limits_{j=0}^\infty {r^j}$ = b, then $\sum\limits_{j=0}^\infty {ar^j}$ = ab. Thus, we will assume that a = 1.

Let s_n = $\sum\limits_{j=0}^n {r^j}$ be the n^th partial sum. Then

Thus

Solving for s_n, we get

and so if |r| < 1

which completes the proof.

Observations

It is pretty easy to see that if r ≥ 1 or r < -1, then the series diverges (i.e. doesn’t converge to a finite value). If r = -1 then the partial sums alternate between 0 and 2, and in this case we consider that the series does not converge to a single finite value.

A simple example of a geometric series is

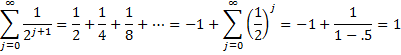Another Key Property

Property 2: If |r| < 1 then the series

Proof: The argument is similar to that used in the proof of Property 1. Let

be the n^th partial sum. Then

Thus

Solving for s_n, we get

and so if |r| < 1, then

which completes the proof.

Examples

From Property 2, we see that

A further example is

This converges to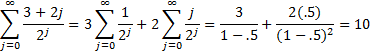 image097c

Reference

Wikipedia (2016) Geometric series
https://en.wikipedia.org/wiki/Geometric_series

Leave a Comment Cancel reply