Nelder-Mead Optimization

Objective

The methods for minimizing a (multivariate) function described elsewhere (for example, by using Newton’s method to find a local minimum), require finding derivatives. We now describe the Nelder-Mead approach that does not require calculating any derivatives.

Our objective is to estimate the values of the column array X with n elements that minimizes f(X).

Methodology

Step 0

We start with a guess consisting of n+1 points X₁, X₂, …, X_n+1 (i.e. one point more than the dimension of X).

The Nelder-Mead algorithm is iterative and consists of several steps, starting with Step 1, as described next. Each step is subdivided into substeps, and the activity to be performed for the 4^th substep depends on several cases (and subcases).

Step 1

Step 1a: Make sure that the n+1 points are sorted such that f(X₁) ≤ f(X₂) ≤ … ≤ f(X_n+1). This ordered set of n+1 points is called a simplex.

Step 1b: Create a centroid which is the mean of the smallest n points, namely

Step 1c: Next calculate the reflection of the worst point, namely

where usually we set ρ = 1.

Substep with cases

Step 1d: Perform one of the following activities depending on the case that applies:

Case 1: If f(X_R) < f(X₁), then test the expansion, namely

where usually we set ψ = 2.

Case 1a: If f(X_E) < f(X_R), then replace X_n+1 by X_E

Case 1b: If f(X_E) ≥ f(X_R), then replace X_n+1 by X_R

Case 2: If f(X_R) < f(X_n), then replace X_n+1 by X_R

Case 3: If f(X_n) ≤ f(X_R) < f(X_n+1), then test the contraction outward, namely

where usually we set γ = .5.

Case 3a: If f(X_C) < f(X_R), then replace X_n+1 by X_C

Case 3b: If f(X_C) ≥ f(X_R), then shrink the simplex, i.e.

where usually we set σ = .5.

Case 4: Otherwise, test the contraction inward, namely

Case 4a: If f(X_I) < f(X_n+1), then replace X_n+1 by X_I

Case 4b: If f(X_I) ≥ f(X_n+1), then shrink the simplex (as described for case 3b)

Step 2, 3, etc.

After step 1 is completed, repeat the same approach in steps 2, 3, etc. on the resulting simplex, until convergence is reached. We will assume that convergence is reached when f(X_n+1) – f(X₁) ≤ ε where ε is some small positive value; we use ε = .000001.

Worksheet Function

The following worksheet functions take lambda function parameters. These are described in Real Statistics Lambda Capabilities and Lambda Functions using Cell Formulas.

Real Statistics Function: The Real Statistics Resource Pack provides the following worksheet function that calculates the local minimum for the function f(X) using the Nelder-Mead algorithm.

Here R1 contains a lambda expression that defines the function f(X) where X is an n-dimensional random vector.

NMEAD(R1, lab, R2, iter, prec): returns an n+2 column array whose first n values consist of the array X where f(X) is minimized, followed by the value f(X) and the number of iterations required until convergence.

If lab = TRUE (default FALSE) a column is appended to the output with labels. iter = the maximum number of iterations for the algorithm (default 150). prec = the convergence criterion  (default .000001). R2 is an optional n × 1 column array that contains one initial guess for X. The remaining n guesses that make up the initial simplex (step 0) are created by an internal algorithm. If R2 is omitted, it defaults to an array whose values are 1, 2, …, n.

Example

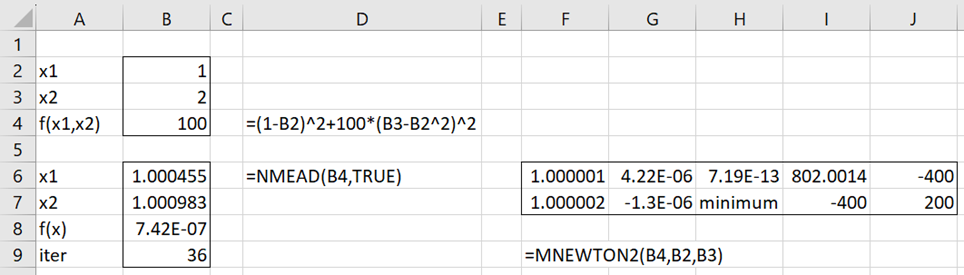
Example 1: Find the value of X that minimizes the function y = f(x₁, x₂) where

Figure 1 shows that the Nelder-Mead algorithm calculates the minimum of f after 36 iterations and that this minimum occurs at (1,1) where f(1,1) = 0. Note that we get the same answer using the MNEWTON2 function.

Figure 1 – Find the minimum using Nelder-Mead

We can use alternative lambda representation in A1:B9 such as

=NMEAD(LAMB(“(1-$x)^2+100*($y-$x^2)^2”),TRUE) or

=NMEAD(LAMB(“(1-x)^2+100*(y-x^2)^2″,”x”,”y”),TRUE).

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Scilab (2010) The Nelder-Mead component
https://scilab.gitlab.io/legacy_wiki/The(20)Nelder(2d)Mead(20)Component

bquanttrading (2016) Nelder-Mead method in VBA
https://asmquantmacro.com/2016/07/01/nelder-mead-method-in-vba/