Basic Concepts
An inflection point c for a function f(x) occurs where f ″(c) = 0. On one side of x = c, the curve of the function is concave up and on the other side, it is concave down.
Identifying an inflection point is a problem when we use Newton’s method to find the root of the derivative f ′(x) since this approach uses the iteration xn+1 = xn – f ′(xn)/f ″(xn). But for xn near the inflection point x = c, thus is close to division by zero.
Example
Example 1: Find the critical points for the function f(x) = x3 – 3x – 3.
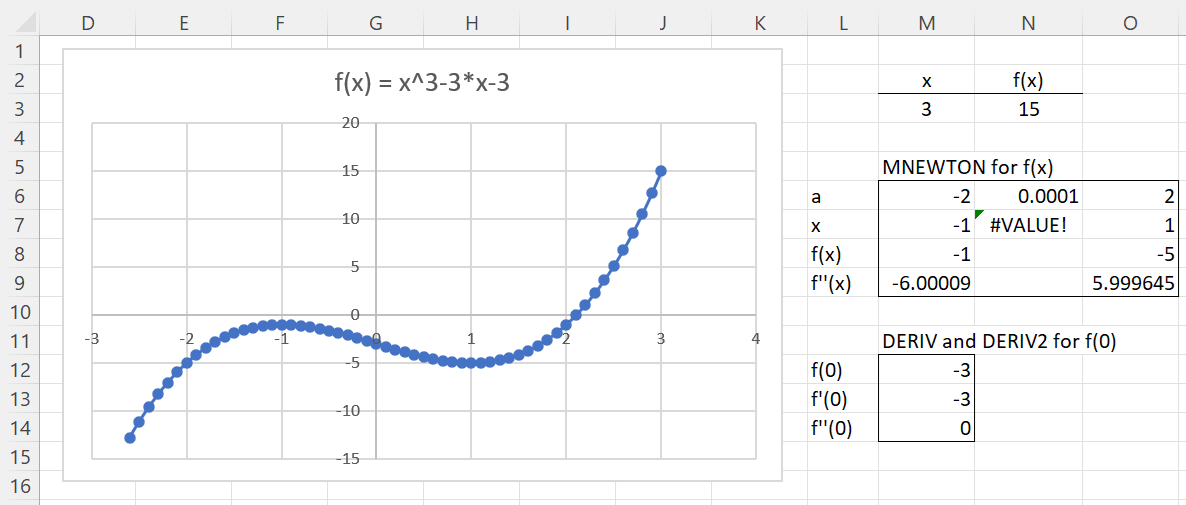
We see from Figure 1 that a local maximum occurs at about x = -1, a local minimum at x = 1, and an inflection point at x = 0.
Figure 1 – Inflection point
We can use the MNEWTON function (see Maxima/minima of a Continuous Function) to confirm the local maximum and minimum. Using an initial guess of -2 we obtain a local maximum at x = -1; using an initial guess of 2, we obtain a local minimum at x = 1. As expected, we get an error value near the inflection point at x = 0 (cell N7).
For example, we use the array formula =MNEWTON(N3,N6) in range N7:N9 where cell N3 contains the formula =M3^3-3*M3-3.
We now observe that f ″(0) = 0 (cell N14) and so x = 0 is an inflection point. Cell N14 contains the formula =DERIV2(0,N3). Also, cell N12 contains the formula =FUNC(0,N3) and cell N13 contains the formula =DERIV(0,N3).
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Reference
Mahaffy, J. M. (2001) Newton’s method – examples
https://jmahaffy.sdsu.edu/courses/f00/math122/lectures/newtons_method/newtonmethodeg.html