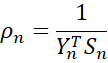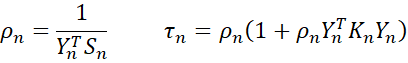Basic Concepts
The Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm provides an effective way to identify a value X that minimizes the multivariate function f(X).
In particular, let f(X) be a function where X is vector of k variables. Our goal is to find a value of X for which f(X) is a local minimum.
Let g(X) be the gradient of f(X) (i.e. a k × 1 matrix of partial derivatives of f at X) and H(X) be the Hessian matrix (i.e. the k × k matrix of partial second derivatives of f at X). The Newton-Raphson method provides an approach for finding a local minimum, but it requires both g(X) and H(X), which may be difficult to obtain. The BFGS algorithm has the advantage that only the gradient is required. The Hessian is estimated numerically.
BFGS Algorithm
The algorithm is iterative. As usual, we start with an initial guess X0 for X, and then define Xn+1 in terms of Xn. The algorithm terminates when a predefined number of steps is completed for convergence is achieved, namely when
||Xn+1 – Xn|| < ε
for some preassigned small positive value ε. Here ||X|| is equal to the sum of squares of the elements in X or the square root of this value.
At each step n, in addition to Xn, we also define the gradient Gn, an approximate Hessian matrix Hn, the inverse Kn of Hn, plus a few other entities (as described below).
Step 0: Initialize X0 and set K0 equal to the k × k identity matrix (actually any positive definite matrix can be used). Note that K0 serves as the initial value of the inverse of the Hessian matrix H0, although we don’t need to calculate the value of any of the Hn.
Step n: Set the gradient Gn = ∇f(Xn) and the direction vector Dn = KnGn.
Next, find αn > 0 that minimizes f(Xn – αnDn).
Set Xn+1 = Xn – αnDn, Sn = Xn+1 – Xn, and Yn = ∇f(Xn+1) – Gn.
It turns out that the inverse of Hn+1 can be calculated by
where
This is called the Sherman-Morrison formula, and is useful since it avoids the computational complexity of finding the inverse of the matrix.
Since Kn is the inverse of Hn, it follows that
where the following scalars are used
Note too that Hn is not needed, only Kn. In fact, only when convergence is reached, do we need to obtain the Hessian via the inverse of Kn.
BTLS Refinement
In the algorithm as described above, we need to find a value of that minimizes . Just as for the gradient descent algorithm, instead of finding the value of that minimizes , it is usually more efficient to use backtracking line search (BTLS) algorithm to set the value of .
This algorithm uses three constants: the initial value λ of αn (usually set to 1), c (usually set to .0001 or .001) and the learning reduction rate ρ (usually set to ½).
The algorithm starts with αn = λ, and tests whether
If this condition is met, then Xn+1 = Xn – αnDn for this value of αn. If not αn is replaced by ραn and the above test is repeated. This process is repeated until the test condition is successful.
Worksheet Function
The Real Statistics Resource Pack provides the following worksheet function.
BGFS(R1, Rx, learn, iter, prec, incr, rrate, c): returns a column array with the value of X that minimizes the function f(X) using BGFS algorithm based on an initial guess of X in the column array Rx where R1 is a cell that contains a formula that represents the function f(X).
See Lambda Functions using Cell Formulas for more details about R1.
learn (default 1) is the initial learning rate, i.e. the parameter λ in the above description. rrate is the learning reduction rate (default .5), i.e. the parameter ρ in the above description. c (default .0001) is the c parameter in the above description.
iter (default 100) = the maximum number of iterations. The algorithm will terminate prior to iter iterations if the error is less than some value based on prec (default .0000001). Since this approach uses the Real Statistics function DERIV to estimate the partial derivatives of the function f(X), the incr parameter used by DERIV needs to be specified (default .000001); See Numerical Differentiation.
Examples
See Gradient Descent Examples for examples of how to use the BFGS algorithm in Excel.
Links
↑ Min/max of a continuous function
References
RTMath (2020) Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm
https://rtmath.net/assets/docs/finmath/html/9ba786fe-9b40-47fb-a64c-c3a492812581.htm
Lam, A. (2020) BFGS in a nutshell: An introduction to quasi-Newton methods
https://towardsdatascience.com/bfgs-in-a-nutshell-an-introduction-to-quasi-newton-methods-21b0e13ee504
Wikipedia (2024) Broyden-Fletcher-Goldfarb-Shanno algorithm
https://en.wikipedia.org/wiki/Broyden%E2%80%93Fletcher%E2%80%93Goldfarb%E2%80%93Shanno_algorithm#:~:text=In%20numerical%20optimization%2C%20the%20Broyden,the%20gradient%20with%20curvature%20information.
Burke, J. (2024) Backtracking line search
https://sites.math.washington.edu/~burke/crs/516/notes/backtracking.pdf
Haghighi, A. (2015) Numerical optimization: understanding L-BFGS
https://aria42.com/blog/2014/12/understanding-lbfgs
Kochenderfer, M, J., Wheeler, T. A. (2019) Algorithms for optimization
https://algorithmsbook.com/files/dm.pdf