Maximum/minimum values of a continuous function

Basic Concepts

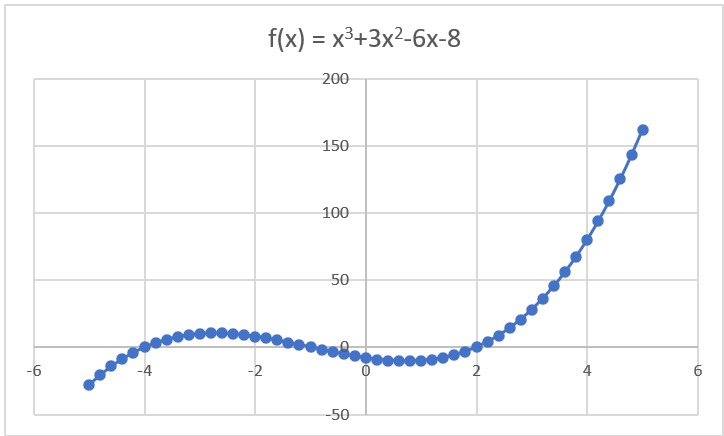
From Figure 1, we see that the function f(x) = x³ + 3x² – 6x – 8 has a local minimum at x = .732051 (i.e. minimum value in the vicinity of this x value) and a local maximum (i.e. maximum value) at x = -2.73205. We will show how we arrived at these specific values shortly. In the interval [-5, 5] neither of these is a global minimum or maximum. In fact, x = -5 is the global minimum and x = 5 is the global maximum.

Figure 1 – Local maximum and minimum

In general, a local minimum or local maximum occurs where the derivative of the function f(x) is zero. For those of you who are not familiar with calculus, all that matters in this context is that this derivative is another function, denoted f ′(x), and we are interested in the roots of this function. The Real Statistics worksheet function DERIV calculates the derivative of a function f(x), and so we need to find the roots of this function. This can be done using the following worksheet function.

Local Minima/Maxima Function

Real Statistics Function: The Real Statistics Resource Pack provides the following worksheet lambda-based function.

MNEWTON(R1, guess, iter, prec, incr, Rx): returns a 3 × 1 column array with a critical value c (based on the initial guess), f(c), and the second derivative of f(x) at c, using Newton’s method.

MNEWTON is used to return a critical value c, which is either a local minimum, a local maximum, or an inflection point for the function f(x). 

The second derivative is used to determine the type of the critical value. If f ′′(c) > 0 then c is a local minimum; if f ′′(c) < 0 then c is a local maximum; if f ′′(c) = 0 then c is an inflection point (see Inflection Point).

R1 is a cell that contains a formula that represents the function f(x) and the address of cell Rx references the variable x in R1. If Rx is omitted, then it defaults to the first cell referenced in R1. See Lambda Functions using Cell Formulas for more details and other options for R1 and Rx.

iter (default 100) = the maximum number of iterations. The algorithm will terminate prior to iter iterations if the error is less than some value based on prec (default .0000001).

guess is the initial guess for the root. Since this approach uses the Real Statistics function DERIV to estimate the derivative of the function f(x), the incr parameter used by DERIV needs to be specified (default .000001); See Numerical Differentiation.

As mentioned above, for those of you who haven’t studied calculus, don’t worry about the concept of a derivative. All you need to know is that the local maxima and minima occur at the roots of the derivative function.

Local Minima/Maxima Example

Example 1: Use the MNEWTON function to find the local minima and maxima for the function f(x) = x³ + 3x² – 6x – 8 illustrated in Figure 1.

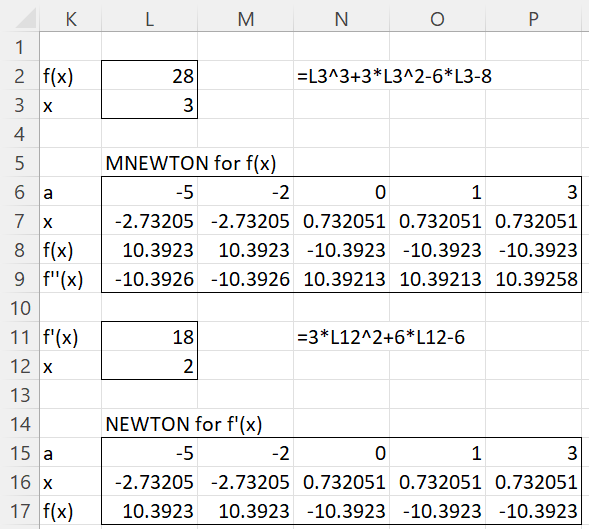
The result is shown in the upper part of Figure 2.

Figure 2 – Local minima and maxima

Here, cell L2 contains the formula =L3^3+3*L3^2-6*L3-8 using L3 as a representative for x. See Lambda Functions using Cell Formulas for more details about this approach.

Row 6 contains various initial guesses for the roots of the derivative f ′(x) and row 7 contains the corresponding root of the derivative function f ′(x). E.g. range L7:L9 contains the array formula =MNEWTON(L2,L6), which indicates that x = -2.73205 is a critical value. Since the value in cell L9 is negative, this means that x = -2.73205 is a local maximum where f(x) = 10.3923 (cell L8). We see that there is also a local minimum at x = .732051 (since the value in cell N9 is positive).

For those of you who are familiar with calculus, the derivative of f(x) is f ′(x) = 3x² + 6x – 6. If we place the formula =3*L36^2+6*L36+6, representing the derivative, in cell L11, we can find the local minima and maxima for f(x) by finding the roots of f ′(x) using the NEWTON function, as shown in row 16. E.g. cell L16 contains the formula =NEWTON(L16,L15). We see that row 16 contains the same results as row 7. In general, we use the MNEWTON function so that we don’t need to calculate the derivative directly.

Options

The lambda-based formula =MNEWTON(L2,L6), described above, can be replaced by alternative forms such as =MNEWTON($L2,L6,,,,L3) or =MNEWTON(“=$x^3+3*$x^2-6*$x-8”,L6) or MNEWTON(“=x^3+3*x^2-6*x-8″,L6,,,,”x”).

Global Minima/Maxima Functions

Real Statistics Functions: The Real Statistics Resource Pack provides the following worksheet lambda-based functions.

FMIN(R1, lower, upper, nguess, iter, prec, incr, Rx) = the global minimum of f(x) in the interval (lower, upper).

FMAX(R1, lower, upper, nguess, iter, prec, incr, Rx) = the global maximum of f(x) in the interval (lower, upper).

The FMAX function calculates the values of f(x₀), f(x₁), …, f(x_n) where n = nguess, x₀ = lower, x_n = upper, x_i+1 = x_i + Δx and Δx = (x_n-x₀)/n, and finds the largest f(x_k) of these values. x_k is then used as an initial guess for MNEWTON to find a possible local maximum. If this value is larger than x_k, then this is likely to be the global maximum. If not then x_k is likely to be the global maxima. FMIN is calculated in a similar manner.

The default for nguess is 1000. The other arguments for FMIN and FMAX are as for MNEWTON.

Global Minima/Maxima Example

Example 2: Use the FMIN and FMAX functions to find the global minima and maxima for the function f(x) from Example 1.

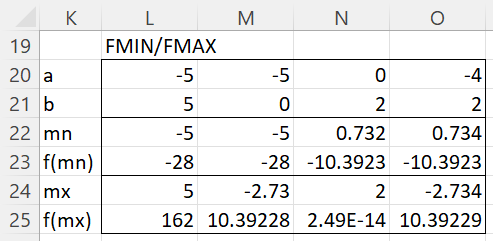
The result is shown in the upper part of Figure 3.

Figure 3 – Global maximum and minimum

We see that on the interval [-5, 5], the global minimum occurs at -5 and the global maximum occurs at 5, but on the interval [-5, 0], the global minimum occurs at -5 and the global maximum occurs at -2.73205. E.g. cell L22 contains the formula =FMIN(L2,L20,L21) and L24 contains =FMAX(L2,L20,L21).

Multivariate Case

See Local Maxima/Minima of a Multivariate Function for information about how to find the local maxima and minima of a continuous function in two or three variables.

See Global Maximum/Minimum of a Multivariate Function for information about how to find the global maximum and minimum of a continuous function in two or three variables.

Also, see Gradient Descent and BGFS Algorithm for information about two other approaches to finding the minimum of a multivariate function.

Finally, see Nelder-Mead Optimization for information about how to find the local minima of a continuous function in one or more variables without using derivatives.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Wikipedia (2021) Newton’s method
https://en.wikipedia.org/wiki/Newton%27s_method

Wikipedia (2021) Maxima and minima
https://en.wikipedia.org/wiki/Maxima_and_minima