Complex Numbers | Real Statistics Using Excel

The set of complex numbers consists of all numbers of the form a + bi where a and b are real numbers and i = $\sqrt{-1}$ . We call a the real part of the complex number and b the imaginary part. We define the absolute value of the complex number to be |a + bi| = $\sqrt{a^2+b^2}$ . The conjugate of the complex number a + bi is a – bi.

Excel Format

In Excel, complex numbers are represented as text of the form “a + bi”. Excel provides a variety of worksheet functions to deal with complex numbers. Most of these begin with the letters “IM”. Some examples are shown in Figure 1. Note that values that are left-justified are text, while values that are right-justified are real numbers.

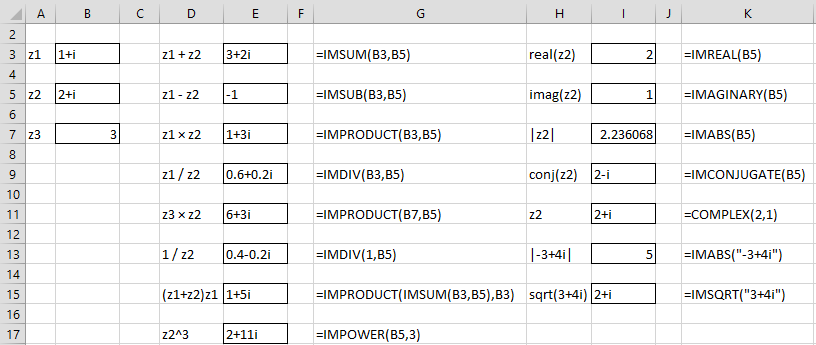
Complex number operations Excel

Figure 1 – Complex number operations in Excel

Excel also provides functions for log (IMLN, IMLOG10, IMLOG2), exponential (IMEXP), various trigonometric functions (IMSIN, IMCOS) square root (IMSQRT), and angle in radians (IMARGUMENT). Additional trigonometric functions are available in Excel 2011, 2013, 2016, 2019, 2021, and 365.

Real Statistics Functions: The Real Statistics Resource Pack supplies the following two additional complex number functions:

IMROOTS(z, n) = column array containing the n unique nth roots of the complex number z

IMROUND(z, n) = the complex number equivalent to z with the real and imaginary parts rounded to n decimal places

Real Statistics Format

Excel does not support complex numbers as numeric values, but we can use a 1 × 2 range to represent the complex number a + bi, where the first cell contains the value for a and the second cell contains the value for b.

We now show how to perform the usual operations on complex numbers and define Real Statistics functions that perform the same operations in Excel.

Addition and subtraction are performed using the usual rules from algebra, as is multiplication where we need to use the fact that i² = -1.

Addition	(a + bi) + (c + di) = (a+c) + (b+d)i
Subtraction	(a + bi) – (c + di) = (a–c) + (b–d)i
Multiplication	(a + bi) · (c + di) = (ac–bd) + (ad+bc)i

Note using the fact that a real number c can be expressed as c + 0i, we see that the multiplication of a complex number by a real number can be expressed as

c · (a + bi) = ac + (bc)i

Note too that

i · (a + bi) = –b + ai

The reciprocal of a complex number is equal to its conjugate divided by the square of its absolute value, as shown by the following

Thus, the division of c + di by a + bi can be accomplished by first expressing the reciprocal of c + di as described above and then multiplying by a + bi.

We can also express raising a complex number z to a positive integer power recursively by performing repeated multiplications: z¹ = z and zⁿ⁺¹ = z · zⁿ. If n is not an integer, then things get a bit more complicated, but we won’t get into that here.

Worksheet Functions

Real Statistics Functions: The Real Statistics Resource Pack supplies the following array functions, where z1, and z2 are 1 × 2 ranges which represent complex numbers and a and b are real numbers. We also suppose that z1 represents the complex number c+di.

CReal(z1) = c	CImag(z1) = d
CAdd(z1, z2) = z1 + z2	CSub(z1, z2) = z1 – z2
CMult(z1, z2) = z1 * z2	CDiv(z1, z2) = z1 / z2
CExp(z1) = exp(z1) = e^z1	CLn(z1) = ln(z1)
CAbs(z1) = \|z1\|	CConj(z1) = c – di
CSet(a,b) = a + bi	CMap(“a+bi”) = a + bi
CPower(z1, n) = z1ⁿ	CText(z1) = “c+di”

Here c–di and a+bi are the 1 × 2 range representations of the corresponding complex number. Note that CReal, CImag, CAbs, CConj, and CText are ordinary functions, while the others are array functions.

A constant complex number can be represented in the form {a, b}. Thus the complex number 3–4i can be represented by {3,-4}. The complex number i can be represented by {0,1} and the complex number 5.2+0i can be represented by {5.2,0} or simply by 5.2.

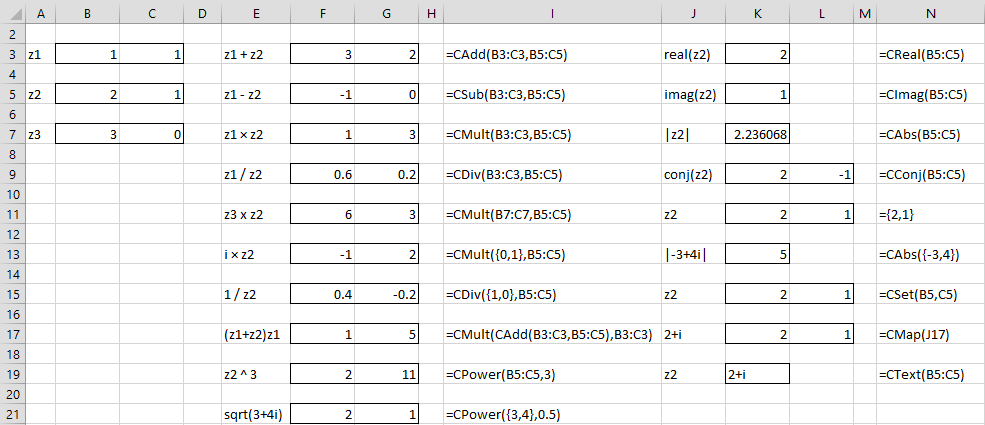
In Figure 2, we show the results of various complex number operations.

Figure 2 – Complex number operations

Observations

CAdd can be used with up to 5 arguments; these arguments can be real or complex numbers: e.g. CAdd(B3:C3, B5:C5, B7:C7) or CAdd(B3:C3, B5, B7:C7,-3). The arguments in CSub can be either complex numbers or real numbers: e.g. CSub(B3:C3, 3) or CSub(F3, B5:C5). The first argument in CDiv can be a complex or real number: e.g. CDiv(1,B5:C5).

Multiplication of a complex number z by a real number a can be accomplished by z * a or CMULT(z, CSet(a,0)). Similarly, the division of a complex number by a real number can be accomplished by z/a or CDiv(z, CSet(a,0)).

You can convert a complex number in Real Statistics format to one in Excel format via the formula =CText(z1), which is equivalent to the formula

=COMPLEX(CReal(z1),CImag(z1))

You can convert from Excel format to Real Statistics format using the array formula =CMap(z1).

Note that for the complex operations not supported by Real Statistics, you can use the Excel functions (when available). E.g. to get the sine of z1 you can use the formula

=CMap(IMSIN(CText(z1))

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Varsity Tutors (2021) Operations with complex numbers
https://www.varsitytutors.com/hotmath/hotmath_help/topics/operations-with-complex-numbers

Prabhat, A. (2021) Basic mathematical operations on complex numbers in Excel
https://quickexcel.com/mathematical-operations-on-complex-numbers

Brenner, S. C., Kaup, D. J. (1999) Introduction to complex numbers
No longer available online