Objective
We show how to perform matrix operations involving complex numbers in Excel. We consider two different formats. On this webpage, we discuss how to perform these operations using Real Statistics format, while in Complex Matrices in Excel Format we describe these operations on matrices in complex numbers in text format “a + bi“.
We represent an m × n matrix of complex numbers by an m × 2n range in Excel. This range consists of an m × n range on the left and another m × n range on the right. The first of these ranges represents the real parts of the values of the complex numbers in the complex number matrix. The second of these ranges represents the imaginary parts of the complex numbers in the complex number matrix.
For example, the complex number matrix
can be represented by the Excel range B13:E14 shown in Figure 1.
Figure 1 – Complex matrix in Excel
The left side in yellow (range B13:C14) contains the real values and the right side in green (range D13:E14) contains the imaginary values.
Essentially, we are expressing a complex matrix as A + Bi where A and B are matrices that only have real values.
Matrix addition, subtraction, multiplication, and inverse on complex matrices are calculated using only real matrix operations, as follows:
![]()
![]()
![]()
Note that the formula for the inverse of a complex matrix requires that both the real part A and imaginary part B be invertible.
Worksheet Functions
Real Statistics Functions: The Real Statistics Resource Pack supplies the following array functions where Z is a range that represents a complex matrix and R and C are arrays that represent real-values matrices.
ZReal(Z) = the real part of the complex matrix Z
ZImag(Z) = the imaginary part of the complex matrix Z
ZSet(R, C) = the complex matrix whose real part is R and whose imaginary part is C
The Real Statistics Resource Pack also supplies the following array functions, where Y and Z are ranges that represent complex matrices, while z is a range that represents a complex (scalar) number and k is a positive integer.
Note that ZIdentity(k) outputs a k × k identity matrix. If k is omitted it defaults to the number of rows in the highlighted range. ZIndex(Z, r, c) returns the complex number in the rth row and cth column of Z. ZConj(Z) returns a matrix of the same size and shape as Z but with every element replaced by the conjugate of that element.
ZLen(V) = the length of the column vector V, i.e. the square root of the sum of the squared absolute values of the entries in V. ZNorm(Z) = the matrix all of whose columns are the normalized versions of the columns in Z (i.e. column vectors divided by their length).
Examples
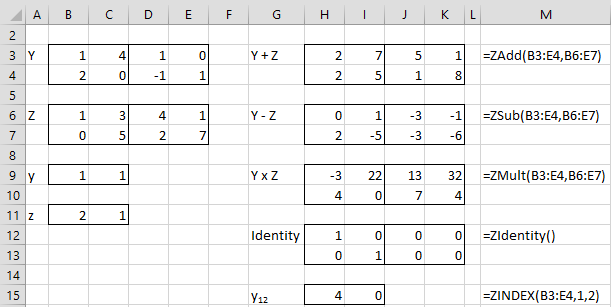
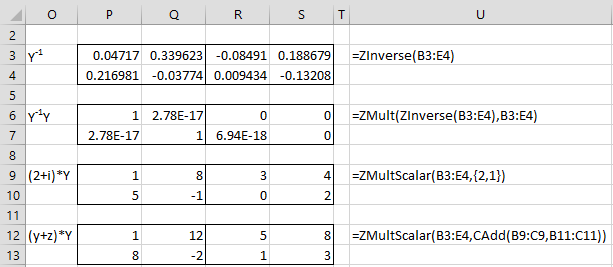
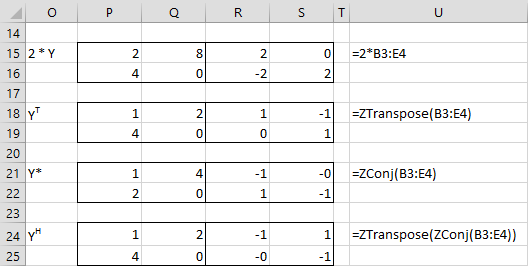
In Figures 2, 3, and 4, we show the results of various complex matrix operations.
Figure 2 – Complex Matrix Operations – part 1
Figure 3 – Complex Matrix Operations – part 2
Figure 4 – Complex Matrix Operations – part 3
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Links
References
Wolfram (2016) Complex matrix
https://mathworld.wolfram.com/ComplexMatrix.html
Brenner, S. C., Kaup, D. J. (1999) Introduction to complex numbers
https://control.dii.unisi.it/sistdin-SI/complex.pdf

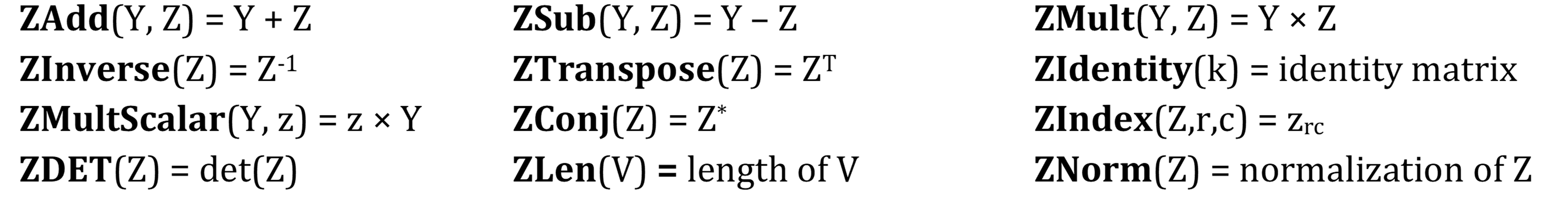
Hi Charles,
I am just starting to use your imaginary matrix manipulation for Excel. I noticed that the complex conjugate and complex conjugate-transpose are missing. Sure, one can just flip the sign of the second part of the matrix for the conjugate matrix but it wouldn’t hurt to include this, since one has to make another copy of the matrix.
With best regards,
Stephan
Hi Stephan,
I will add this in the next release of the software. Thanks for your suggestion.
Note that there is an error in the ZMultScalar function that will also be corrected in the next release.
Charles
Thanks for your reply. I also noticed that the complex determinant is missing, too.
Ok Stephan, I will add the determinant as well in the next release.
Charles
Hi Charles
My Excel 395 keeps crashing when I open a spreadsheet that uses the real-statistics tools. I have to deselect the tools under the Add-In option, close Excel, then open Excel and reselect it to work. Also the Solver tool gives me error messages, I am not sure if that is related to the real-statistics tool, I am using a brand-new MS surface laptop, maybe the Excel installation is still buggy…
Thanks!
Stephan,
I suggest that you first disable Real Statistics and resolve the problem with Solver. To disable Real Statistics, just press Alt-TI and uncheck RealStats in the list of addins. If the problem with Solver disappears after disabling Real Statistics, then I suggest that you enable RealStats and then press Ctrl-m to see whether you can access the Real Statistics main menu.
Charles
One more question please. In Excel Spreadsheet calculations, do we use in the complex numbers imaginary part radians or degrees for the phase evaluation?
Dash
Dash,
Radians.
Charles
P.S. BTW I wrote my own subtraction routine. It is faster that way. :-). Still you should investigate my error or a possible bug ?
Dash
Dash,
Glad to see that you were able to create your own routine.
Unfortunately, I am not sure how to interpret your data, and so I am not able to reproduce the error.
Charles
A simple question: How do I attach my excel file into this note format?
Perhaps you could send me
your e-mail address given in my registration.
Dash
Dash,
You can find my email address at Contact Us.
Charles
Why the command “=ZSUBScalar(C1:D200,E1:F200)” or ZSUB(C1:D200,E1:F200) neither IMSUB(C1:D200,E1:F200) do not work and show “#NAME?” error in each case?
Could you please help me with this error or refer me to an appropriate site. Excel 2013
Thank you
Dash
Dash,
If you send me an Excel file with your data and the output you obtained, I will try to figure out what is going wrong.
Charles
Hi Charles,
Thank you for your answer. I’ve got it somewhat working, however when I use =ZSub(B1:C200,D1:E200) I get only one number (I think it is vector R from complex notation. I have not checked it, sorry. Even using ZSub(B1:C1,D1:E1) results in a single notation number, i.e x. After performing my subtraction I need a complex number.
Could you please explain why I am not getting as a number in the form x+iy ?
Thank you in advance for your help in this matter.
Here is some of my input data:
3.34E-05 -43.1349 6.46E-05 -18.0324
3.61E-05 -81.553 5.44E-05 -34.8703
3.87E-05 -114.2756 4.02E-05 -49.5775
4.06E-05 -142.5748 2.41E-05 -60.5245
4.17E-05 -169.8514 8.00E-06 -53.3559
4.12E-05 165.4471 1.11E-05 58.2968
3.99E-05 139.1623 2.73E-05 57.5078
3.76E-05 110.0261 4.30E-05 45.6528
3.49E-05 76.1881 5.65E-05 30.6889
3.26E-05 36.5155 6.56E-05 13.7571
3.23E-05 -7.1469 6.82E-05 -4.2803
3.42E-05 -49.5328 6.32E-05 -22.2475
3.72E-05 -86.7053 5.21E-05 -38.9449
3.97E-05 -118.4557 3.72E-05 -53.3403
4.12E-05 -146.3252 2.08E-05 -63.1576
4.16E-05 -172.1025 5.38E-06 -36.5526
4.08E-05 162.5052 1.44E-05 59.2935
3.91E-05 135.7654 3.06E-05 54.1452
3.67E-05 105.4257 4.62E-05 40.7421
3.36E-05 70.9739 5.79E-05 26.8037
Dash
Dash,
If you send me an Excel file with your data and the output you obtained, I will try to figure out what is going wrong.
Charles