There is also a three-parameter version of the Weibull distribution, which adds a location parameter γ. The probability density function (pdf) of this distribution is
for x ≥ γ. Here β > 0 is the shape parameter and α > 0 is the scale parameter.
The cumulative distribution function (cdf) is
The inverse cumulative distribution function is
Thus, we can calculate the pdf and cdf in Excel by the following formula:
WEIBULL.DIST(x–γ, β, α, cum)
where if cum = TRUE, then the cdf is calculated, and if cum = FALSE then the pdf is calculated. We can also use the following Real Statistics formula to calculate the inverse function.
WEIBULL_INV(p, β, α) + γ
Key statistical properties of the 3-parameter Weibull distribution are:
Figure 1 – Statistical properties
Reference
Wikipedia (2021) The Weibull distribution
http://reliawiki.org/index.php/The_Weibull_Distribution
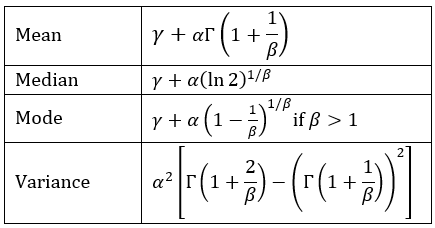
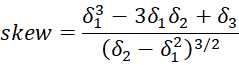
In Figure 1, are you assuming that the mu in the variance equation is the mean that is presented in that same figure? If so, I believe that is incorrect. The variance equation should not depend on the gamma parameter.
Hi Nancy,
Yes, you are correct. I have now revised the figure.
Thank you very much for pointing out this mistake.
Charles
The Mode equation in Figure 1 is incorrect. the 2nd term should be multiplied by alpha.
Thanks, Bruce for bringing this to my attention. I have corrected the error.
I appreciate your help in improving the accuracy of the website.
Charles
Hi
My name is Ki Jong. Can i get an advice from you?
I conducted experiment on sloshing.
From the experimental data, I wanna to fit the data using 3-parameters Webull distribution by means of excel. X axis is peak pressure and Y axis is probability.
But, it is not working. can I get your email in order to explain my problems?
Hello Ki Jong,
Real Statistics doesn’t yet provide any support for fitting data to a three-parameter Weibull distribution. The website shows three different ways for fitting data to a two-parameter Weibull distribution.
Charles
Hi Charles
Do you plan to work on the mixed weibull distribution?
Kind regards,
Vincent bour
Hi Vincent,
I will add this to the list of possible future enhancements.
Charles
It will be very usefull for me considering the number of unknown parameters that we have to found via MLE ?