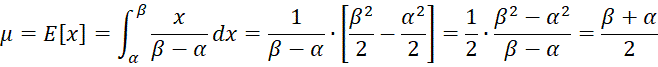Property A: The moment generating function for the uniform distribution is
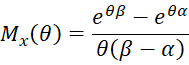
Proof:
Property B: The mean for a random variable x with uniform distribution is (β–α)/2 and the variance is (β–α)2/12.
Proof:
Now
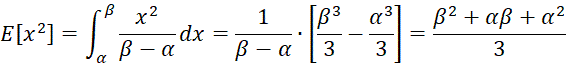Thus
Property 1 of Order statistics from finite population: The mean of the order statistics from a discrete distribution is
Proof: The proof is by induction on k.
Property 2 of Order statistics from continuous population: The pdf of the kth order statistic is
Proof: We use the fact that the pdf is the derivative of the cdf.
By Property 1 of Order statistics from continuous population, the cdf of the kth order statistic is
Now
We now claim that the two sums in the last expression cancel each other out, leaving only the first expression, which is the desired result. To see that the difference between the last two sums is zero, make a change of variables in the last sum by replacing i by j-1. In this way the last sum becomes
References
Ma D. (2010) The distribution of the order statistics. A Blog on probability and statistics
https://probabilityandstats.wordpress.com/2010/02/20/the-distributions-of-the-order-statistics/
Border, K. C. (2016) Lecture 15: Order statistics; conditional expectation. Caltech
https://healy.econ.ohio-state.edu/kcb/Ma103/Notes/Lecture15.pdf
Rundel, C. (2012) Lecture 15: order statistics. Duke University
https://www2.stat.duke.edu/courses/Spring12/sta104.1/Lectures/Lec15.pdf