Basic Concepts
Asking for a random set of say 100 numbers between 1 and 10, is equivalent to creating a sample from a continuous uniform distribution, where α = 1 and β = 10 according to the following definition.
Definition 1: The continuous uniform distribution has the probability density function (pdf)
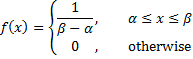
where α and β are any parameters with α < β.
The corresponding cumulative distribution function (cdf) is
The inverse cumulative distribution function is
I(p) = α + p(β − α)
Properties
Key statistical properties are shown in Figure 1.
Figure 1 – Statistical properties of the uniform distribution
Observation: A continuous uniform distribution in the interval (0, 1) can be expressed as a beta distribution with parameters α = 1 and β = 1.
Worksheet Functions
Real Statistics Functions: Excel doesn’t provide any functions for the uniform distribution. Instead, you can use the following functions provided by the Real Statistics Resource Pack.
UNIFORM_DIST(x, α, β, cum) = the pdf of the continuous uniform distribution f(x) at x when cum = FALSE and the corresponding cumulative distribution function F(x) when cum = TRUE.
UNIFORM_INV(p, α, β) = x such that UNIFORM_DIST(x, α, β, TRUE) = p. Thus UNIFORM_INV is the inverse of the cumulative uniform distribution
Examples
Example 1: A bus arrives regularly every 20 minutes throughout the day. What is the probability that you will have to wait more than 15 minutes assuming that you arrive at a random time?
Let x = the time that you arrive in the interval a = 0 to b = 20. The random variable has a uniform distribution. Thus, the probability that you will wait at most 15 minutes is F(15) = (–a)/(b–a) = (15–0)/(20–0) = .75. This means that the probability that you will need to wait more than 15 minutes is 1 – .75 = .25.
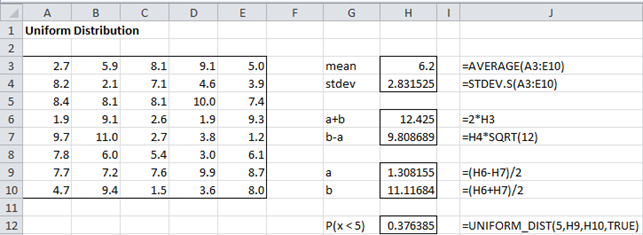
Example 2: A random sample of size 40 is taken from a population with a uniform distribution as shown in range A3:E10 of Figure 2. What is the probability that any random sample element will be less than 5?
Figure 2 – Uniform distribution example
This is similar to Example 1 except that we don’t know the values of the endpoints a and b of the uniform distribution. We begin by calculating the sample mean and standard deviation (cells H3 and H4 of Figure 2). We assume that these are reasonable estimates of the population mean and standard deviation.
From Figure 1 we see that the 12.425 = 2μ = a + b and 9.809 = √12 σ = b – a. Solving these simultaneous equations for a and b, we get a = 1.308 and b = 11.117. Let x be the value of an element randomly drawn from the distribution. The probability that x < 5 can be calculated by the formula =UNIFORM_DIST(5, a, b,TRUE), which is 37.6% as shown in cell H12 of Figure 2.
Related Topics
There is also a discrete version of the uniform distribution. Related to the uniform distributions are order statistics. Click on any of the following links for more information:
- Discrete Uniform Distribution
- Triangular Distribution
- Distribution of order statistics from a discrete population
- Distribution of order statistics from a continuous population
- Proofs
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Reference
Wikipedia (2012) Continuous uniform distribution
https://en.wikipedia.org/wiki/Continuous_uniform_distribution
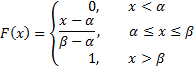

Can you please mention the formula for it?
UNIFORM_INV(p, α, β) = x such that UNIFORM_DIST(x, α, β, TRUE) = p. Thus UNIFORM_INV is the inverse of the cumulative uniform distribution
Yours,
Matin
Hello Matin,
The formula is shown on the webpage, namely I(p) = α + p(β − α).
Charles
Excel does not have the function for uniform distribution. I wonder why given that it should not be too difficult to put this function when it has all the other ones with more complex cases!
I don’t know, but maybe because such a function is not so complicated to replace by a formula.
Charles
Can I know the exact formula for the inverse of the cumulative uniform distribution, using p, α, β, please?
Hello Matin,
The formula is shown on the webpage, namely I(p) = α + p(β − α).
Charles
Hey
If i make 200 observations and 2 columns (size = 2) of a uniform distribution between 4 and 7 and i wanted to get the mean, do i use the function average in excel or do i use:
Mean = (α + β) / 2 ?
regards
Heba
i mean if i wanted to get a 200 observations means so each two values from column A and B i get their mean. so i can graph the means
Regards
Heba
Heba,
You would use AVERAGE in this case. With only two means, the graph may not be that interesting.
Charles
Hello Heba,
If you want to get the sample mean then use the AVERAGE function on the 200 observations.
If you want to get the population mean when the alpha and beta parameters are known then use (α + β) / 2.
Charles
How to create data sets that is uniforms drawn from [5, 10) in excel?
Repeatedly use the following formula: =5+(10-5)*RAND()
Charles
Is it possible to sample data instances using a distribution different from the uniform distribution? If so, give an example of a probability distribution of the data instances that is different from uniform (i.e., equal probability).
Hello Praveen,
Yes, you can. E.g. to create a 10 element sample from the standard normal distribution, place the formula =NORM.S.INV(RAND()) in cell A1, highlight the range A1:A10 and press Ctrl-D.
Charles
My question is ( does rectangular distribution haveno mode or any values between alpha and beta.) ???
Any value between alpha and beta.
Charles
Hello,
My Excel doesn’t recognize the UNIFORM_INV after installing and checking it on in Excel 2016.. What can I do? (VER() doesn’t work as well)
This probably means that you haven’t installed the Real Statistics addin. These are not standard Excel capabilities. You need to download the Real Statistics addin. It is free.
Charles
Just type RAND()*(b-a) + a. Don’t need to download any package.
I’ve downloaded the Resource Pack and ticked the Realstats add-in but excel isn’t recognising UNIFORM_DIST as a formula. Any ideas/tips on what I may be doing wrong?
Ben,
What do you see when you enter the formula =VER()
Charles
Just type RAND()*(b-a) + a. Don’t need to download any package.
Charles,
First of all thank you for porting your add-in to excel 2016. Now I have opportunity to use it. I’ve recently installed it and currently trying to learn it’s functionality . I’ve found problem with UNIFORM_DIST function.
I make a table with two columns. First column is x values. Second column: UNIFORM_DIST(first_column_value_of_same_row,1,3,0). Third row: UNIFORM_DIST(first_column_value_of_same_row,1,3,1).
0 0 0
1 0.5 0
2 0.5 0.5
3 0.5 1
4 0 1
Problem: probabilities in second column don’t sum up to 1. Also the third row is made considering (α, β] interval (so α is not included – I’m not sure if that’s intentional)
Artem,
The correct form of the formula is UNIFORM_DIST(x,0,3,cum). Thus the table should look like
x pdf cdf
0 0.333333333 0
1 0.333333333 0.333333333
2 0.333333333 0.666666667
3 0.333333333 1
Charles
Just type RAND()*(b-a) + a. Don’t need to download any package.
Resp. Sir
I want to generate U(0,1),with 50 size.where p1=2*p2,p2=p3 and p4=1-(p1+p2+p3).
Use the monte carlo method to optimize n1,n2,n3 and n4.Give early as possible.
Gopal,
You have repeated this problem to me several times now, but I am sorry to say that I still don’t understand the question well enough to give you an answer.
Charles
Sir,I want to generate U(0,1),for sample size 50 with between 0.72 to 0.92 where p2=p3,p1=2*p2 and p4=1-(p1+p2+p3).Optimize sample size with n1,n2,n3 and n4.Is it possible in Excel 2007.Give me help
You can certainly generate a sample of size 50 that follows a uniform distribution U(0,1), namely by using the RAND() formula, but I don’t understand the other constraints that you have listed.
Charles
Resp.Sir,
I have applied Multinomial Distribution.I have to generate the probabilities p1+p2+p3<=0.8 and p1=2p2=2p3.Generate 50 random nos using U(0,1).Obtain p1,p2,p3.Then using Monte-Carlo Method and estimate n1,n2,n3.Is it possible in Excel 2007
Resp.Sir,
I have applied Multinomial Distribution.I have to generate the probabilities p1+p2+p3<=0.8 and p1=2p2=2p3.Generate 50 random nos using U(0,1).Obtain p1,p2,p3.Then using Monte-Carlo Method and estimate n1,n2,n3.Is it possible in Excel 2007
Reply
how to do monte carlo simulation in excel 2007 and how to calculate prediction using uniform distribution
Revathi,
See the following webpage: Simulation.
Charles
I have generated the UNIFORM_DIST value. Now how do I get the graph in excel for presentation.
Avi,
The following approach can be used to generate a graph of any distribution with probability density function f(x) in Excel in say the range a to b. For simplicity I will assume that a = 2 and b = 5. I will also assume that you want the granularity of the graph to be in units of size .1 (you can choose whatever granularity you like).
Place the value of 2 (i.e. a) in cell A1. Next place the formula =A1+.1 in cell A2 (here .1 is the granularity). Next highlight the range A2:30 and press Ctrl-D. This will place the numbers 2, 2.1, 2.2, …, 4.9, 5.0 in the range A1:A31 (here 5 is b). Next, place the formula for f(x) in cell B1 where x is replaced by the cell reference A1 — for your problem you use UNIFORM_DIST(A1,2,5,FALSE). Now highlight the range B1:B31 and press Ctrl-D. Finally, highlight the range A1:B31 and create a scatter plot by choosing Insert > Charts|Scatter.
The resulting graph will be the horizontal line y = 1/3 between 2 and 5. In general the graph will be the horizontal line y = 1/(b-a) between x = a and x = b.
Charles
Dear Charles,
I am trying to generate a CDF with a uniform distribution between -55 and -45 with 1000 samples. I can’t seem to get the function to work. I typed in uniform_dist(1000,-55,-45,true), and all I seem to be getting is 1’s. Am I doing something wrong?
Regards,
Raquel
Raquel,
Since the first argument (1000) is larger than the third argument(-45), the cdf is always 1. Generally you should choose a value for the first argument that is between the second and third arguments. E.g. uniform_dist(-51,-55,-45,true) has the value .4
Charles
Just type RAND()*(b-a) + a. Don’t need to download any package.
Dear Charles,
I’ve been browsing your site in search for a solution to my question. But I am unsure what method to employ.
I am working in Excell. My sample consists of 66 columns and 250 rows. Of the 1650o datapoints, 290 display a one; the rest are zero.The distribution of 1’s over the 66 columns is relevant to me and I wish to determine whether this distribution is statistically different from a random distribution.
Could you please give me some pointers (binom/poisson/normal dist?; How can I efficiently perform simulations?)
Kind regards,
Antoine
Antoine,
See the webpage https://real-statistics.com/sampling-distributions/simulation/ for information about simulations
See the webpage https://real-statistics.com/non-parametric-tests/one-sample-runs-test/ for information about testing random runs of 0’s and 1’s
Charles