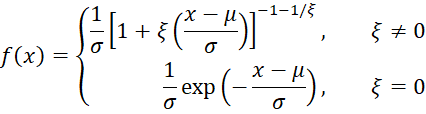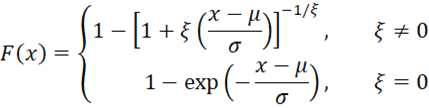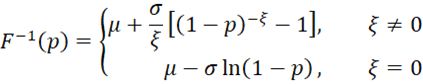Basic Concepts
The probability density function (pdf) of the Generalized Pareto distribution GPD(μ, σ, ξ) with location parameter μ, scale parameter σ > 0, and shape parameter ξ is
The cumulative distribution function is
The pdf and cdf are defined for x ≥ μ when ξ ≥ 0 and for μ – σ/ξ > x ≥ μ when ξ < 0.
The inverse of the cdf is
Applications
The Generalized Pareto distribution is used to model the distribution of the tail of another distribution; i.e. the value x ≥ some threshold value μ. The choice of the shape parameter, ξ, depends on the type of distribution whose tail is being modeled. For example
- ξ = 0 for distributions whose tails decrease exponentially (e.g. the normal distribution)
- ξ > 0 for distributions whose tails decrease as a polynomial (e.g. the t distribution)
- ξ < 0 for distributions whose tails are finite (e.g. the beta distribution)
Properties
Figure 1 displays the key properties of the Generalized Pareto distribution.
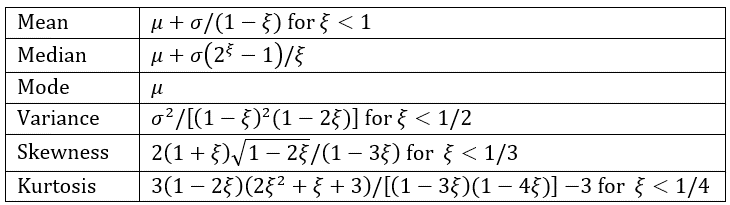
Figure 1 – GPD key properties
Property 1: If ξ > 0 then GPD(m,m/α,1/α) = Pareto distribution with parameters m and α.
Proof: We first note that m/α =mξ. We now match the cdf as follows:
Property 2: GPD(0,σ,0) = Exponential distribution with rate parameter 1/σ.
Proof: Similar to the proof of Property 1.
Worksheet Functions
Real Statistics Functions: The Real Statistics Resource Pack provides the following functions.
GPD_DIST(x, μ, σ, ξ, cum) = the pdf of the GPD when cum = FALSE and the corresponding cumulative distribution function when cum = TRUE.
GPD_INV(p, μ, σ, ξ) = the inverse of the GPD at p
Distribution Fitting
Click here for information about how to fit data to a GPD using the method of moments.
References
Mathworks (2022) Generalized Pareto distribution
https://www.mathworks.com/help/stats/gpcdf.html
Wikipedia (2022) Generalized Pareto distribution
https://en.wikipedia.org/wiki/Generalized_Pareto_distribution