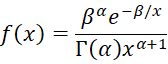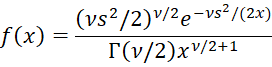We now briefly describe three distributions that are useful in Bayesian statistics.
Inverse Gamma Distribution
The pdf of the Inverse Gamma distribution for x > 0 with shape parameter α and scale parameter β is
where α > o and β > 0. The cdf of the inverse gamma distribution is
F(x) = 1–GAMMA.DIST(1/x, α, 1/β, TRUE)
or equivalently
F(x) = Γ(α, β/x)/Γ(α)
where Γ(α, β) is the upper gamma function as described at Gamma Function Advanced and calculated by the Real Statistics function UpperGamma(α, β).
The inverse of the distribution is given by
F-1(p) = 1/GAMMA.INV(1-p, α, 1/β)
Note that if x has a gamma distribution with shape parameter α and scale parameter β, 1/x will have an inverse gamma distribution with shape parameter α and scale parameter 1/β.
Figure 1 displays key properties of the inverse gamma distribution.
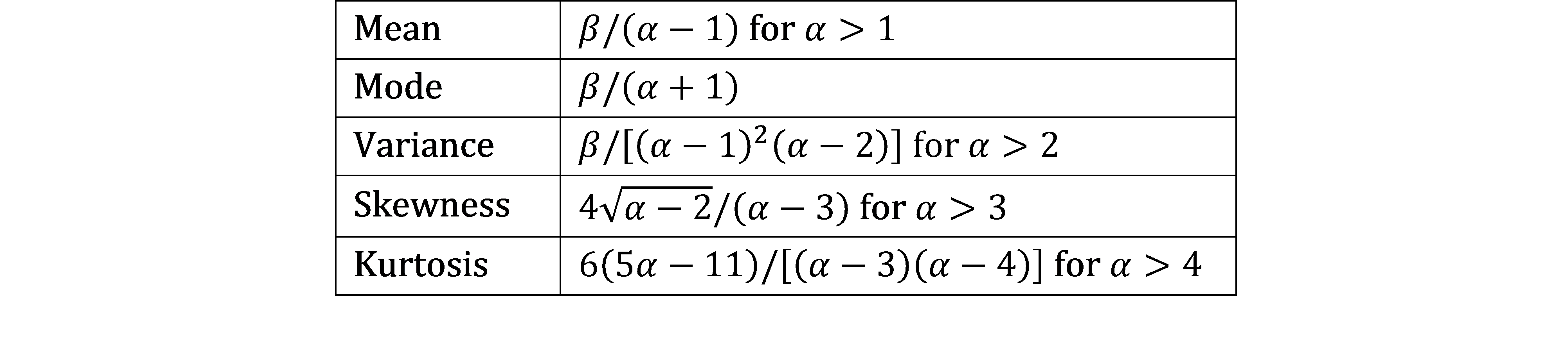Figure 1 – Properties of the Inverse Gamma distribution
Real Statistics Functions: The Real Statistics Resource Pack provides the following functions for the Inverse Gamma distribution.
IGAMMA_DIST(x, α, β, cum) = the pdf of the Inverse Gamma distribution f(x) when cum = FALSE and the corresponding cumulative distribution function F(x) when cum = TRUE.
IGAMMA_INV(p, α, β) = the inverse of the Inverse Gamma distribution at p
Inverse Chi-square Distribution
The pdf of the Inverse Chi-square distribution for x > 0 with ν degrees of freedom is
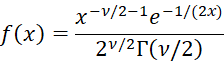
where ν > 0. Since x has an inverse chi-square distribution with ν degrees of freedom if and only if 1/x has a chi-square distribution with ν degrees of freedom, the cdf is
F(x) = CHISQ.DIST.RT(1/x, ν)
Similarly, the inverse of the distribution is given by
F-1(p) = 1/CHISQ.INV.RT(p, ν)
Also, note that x ∼ Inv-χ2(ν) is equivalent to x ∼ Inv-Gamma(ν/2, 1/2). Thus ICHISQ_DIST(x, ν, cum) and IGAMMA_DIST(x, ν/2, 1/2, cum) yield the same values.
Figure 2 displays key properties of the inverse chi-square distribution.
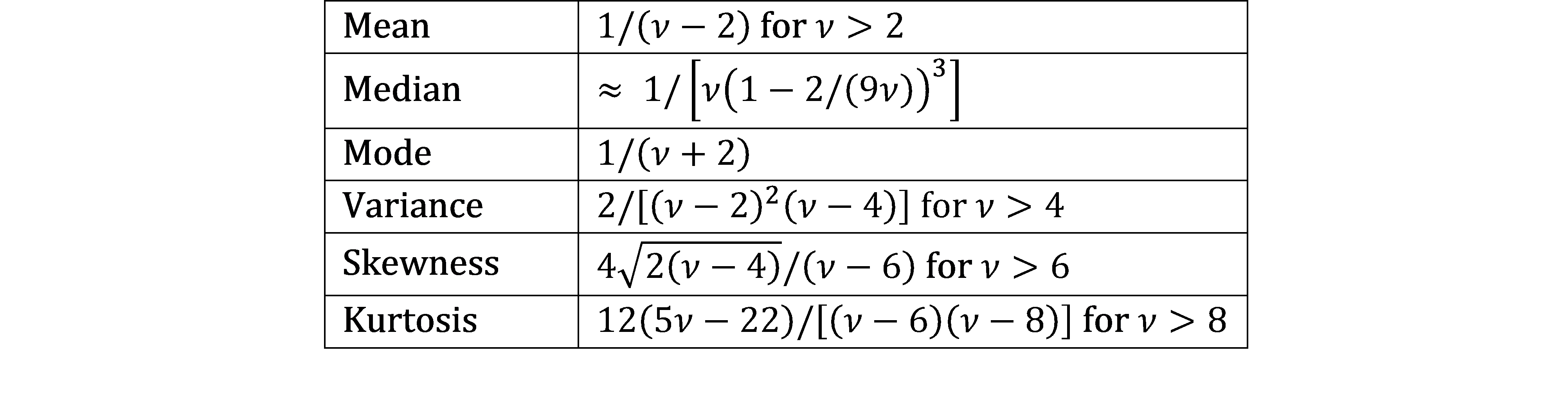Figure 2 – Properties of the Inverse Chi-square distribution
Real Statistics Functions: The Real Statistics Resource Pack provides the following functions for the Inverse Chi-square distribution.
ICHISQ_DIST(x, df, cum) = the pdf of the Inverse Chi-square distribution f(x) when cum = FALSE and the corresponding cumulative distribution function F(x) when cum = TRUE.
ICHISQ_INV(p, df) = the inverse of the Inverse Chi-square distribution at p
Scaled Inverse Chi-square Distribution
The pdf of the Scaled Inverse Chi-square distribution for x > 0 with ν degrees of freedom and scale parameter s2 is
where s > 0 and ν > 0.
Note that the pdf of the inverse chi-square distribution with ν degrees of freedom is the same as the pdf of the scaled inverse chi-square distribution with ν degrees of freedom and a scale parameter of 1/ν.
Note too that x ∼ Scaled-Inv-χ2(ν, s2) is equivalent to x/(νs2) ∼ Inv-χ2(ν).
Also, x ∼ Scaled-Inv-χ2(ν, s2) is equivalent to x ∼ Inv-Gamma(ν/2, νs2/2).
Thus, the cdf of the scaled inverse chi-square distribution can be expressed as
F(x) = IGAMMA.DIST(x, ν/2, νs2/2, TRUE)
Similarly, the inverse of the distribution can be expressed as
F-1(p) = IGAMMA.INV(p, ν/2, νs2/2)
Figure 3 displays key properties of the scaled inverse chi-square distribution.
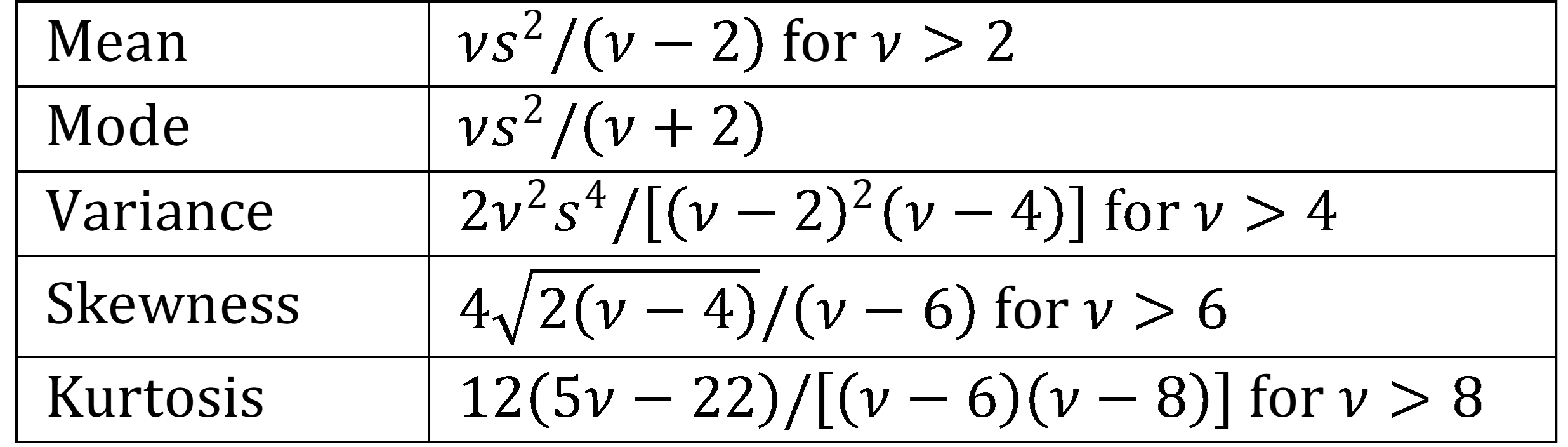
Figure 3 – Properties of the Inverse Chi-square distribution
Real Statistics Functions: The Real Statistics Resource Pack provides the following functions for the Scaled Inverse Chi-square distribution.
SICHISQ_DIST(x, df, s2, cum) = the pdf of the Scaled Inverse Chi-square distribution f(x) when cum = FALSE and the corresponding cumulative distribution function F(x) when cum = TRUE.
SICHISQ_INV(p, df, s2) = the inverse of the Scaled Inverse Chi-square distribution at p
References
Wikipedia (2020) Inverse gamma distribution
https://en.wikipedia.org/wiki/Inverse-gamma_distribution
Wikipedia (2020) Inverse chi-square distribution
https://en.wikipedia.org/wiki/Inverse-gamma_distribution
Wikipedia (2020) Scaled inverse chi-square distribution
https://en.wikipedia.org/wiki/Scaled_inverse_chi-squared_distribution
Cook, J. D. (2008) Inverse gamma distribution
https://www.johndcook.com/inverse_gamma.pdf