Gumbel Distribution

Objective

We use the Gumbel distribution to model the largest value from a relatively large set of independent elements from distributions whose tails decay relatively fast, such as a normal or exponential distribution. As a result, it can be used to analyze annual maximum daily rainfall volumes. In this way, it can be used to predict extreme events such as floods, earthquakes, or hurricanes.

For this reason, the Gumbel distribution is also called the extreme value type I distribution and is used to find a maximum extreme value. Setting x to –x will find the minimum extreme value.

Properties

The pdf of the Gumbel distribution with location parameter μ and scale parameter β is

where β > 0. The cdf is

The inverse of the Gumbel distribution is

The standard Gumbel distribution is the case where μ = 0 and β = 1.

The Gumbel distribution is sometimes called the double exponential distribution, although this term is often used for the Laplace distribution.

Key statistical properties of the Gumbel distribution are:

Figure 1 – Statistical properties of the Gumbel distribution

Here, γ is the Euler-Mascheroni constant whose value is –ψ₀(1), the negative of the digamma function at 1 (see MLE Fitting Gamma Distribution) with a value approximately equal to .577215665.           

Graphs                                              

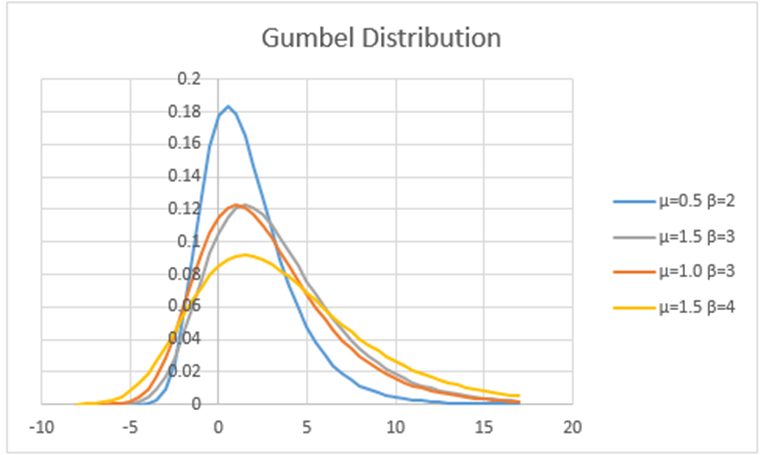
Figure 2 shows a graph of the Gumbel distribution for different values of μ and β.

Figure 2 – Chart of the Gumbel distribution

Worksheet Functions

Real Statistics Functions: The Real Statistics Resource Pack provides the following functions for the Gumbel distribution.

GUMBEL_DIST(x, μ, β, cum) = the pdf of the Gumbel distribution f(x) when cum = FALSE and the corresponding cumulative distribution function F(x) when cum = TRUE.

GUMBEL_INV(p, μ, β) = the inverse of the Gumbel distribution at p

Relationship with other distributions

Property 1: If x ∼ Weibull(α, β) then β(1 – α ln(x/α)) ∼ Gumbel(α, β)

It also follows that if x ∼ Gumbel(μ, β) then β exp(-(x-μ)/(βμ)) ∼ Weibull(μ, β) 

Property 2 (Fisher-Tippett-Gnedenko): If {x₁, …, x_n} is a random sample from a standard normal distribution and x_(n) is the maximum value from this sample (i.e. the nth order statistic), then x_(n) ∼ Gumbel(μ, β) where

μ = NORM.S.INV(1 – 1/n)          β = NORM.S.INV(1 – 1/(ne)) – μ

Example 1: What is the expected maximum value of a sample of size 10 taken from a normal distribution with mean 1 and standard deviation 2?

If {x₁, …, x₁₀} is such a random sample, then {z₁, …, z₁₀}, where z_i = (x_i–1)/2, comes from a standard normal distribution. The maximum of the original series x₍₁₀₎ = 2z₍₁₀₎ + 1.

By Property 2, we know that z₍₁₀₎ has a Gumbel distribution with

μ = NORM.S.INV(1 – 1/10)  = 1.281552

β = NORM.S.INV(1 – 1/(10e)) – μ = 1.789242 – 1.281552 = .507690

Thus, the mean of z₍₁₀₎ is equal to

μ + βγ = 1.2881552 + .507690 ⋅ .577215665 = 1.574598

and so the expected value of the largest value in the original sample is

mean of x₍₁₀₎ = 2⋅ mean of z₍₁₀₎ + 1 = 2⋅ 1.574598 + 1 = 4.149197

Property 3: If x and y are independent, x ∼ Gumbel(μ_x, β) and  y ∼ Gumbel(μ_y, β) then y – x ∼ Logistic(μ_y–μ_x, β)

Property 4: If x has a Weibull distribution, then -ln(x) has a Gumbel distribution.

Property 5: If x has an exponential distribution with mean 1, then ln(x) ∼ Gumbel(0,1).

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Wikipedia (2020) Gumbel distribution
https://en.wikipedia.org/wiki/Gumbel_distribution

Hastings, N., Peacock, B. (2011) Statistical distributions. 4th Ed, Wiley
https://www.wiley.com/en-us/Statistical+Distributions%2C+4th+Edition-p-9780470390634