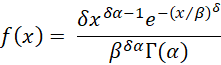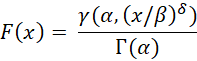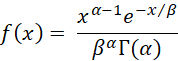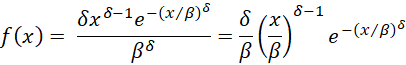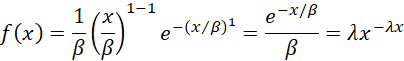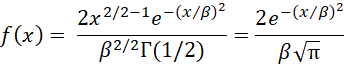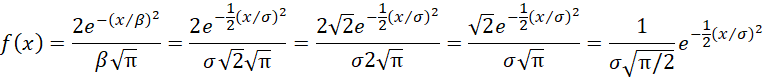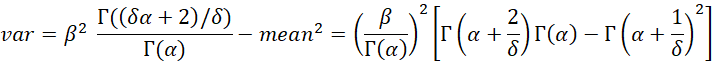Basic Concepts
The generalized gamma distribution is a three-parameter version of the gamma distribution. It adds a second shape parameter δ. A number of distributions besides the gamma distribution are special cases of this distribution.
The probability density function (pdf) of the generalized gamma distribution is
In this case, we use the notation x ~ G(α, β, δ).
The cumulative distribution function (cdf) is given by
where γ(α, z) is the lower incomplete gamma function (see Gamma Function Advanced).
If x has a gamma distribution, then x ~ G(α, β, 1), and so, the pdf is
as expected.
Properties
Property 1: If k > 0 and x ~ G(α, β, δ), then
kx ∼ G(α, kβ, δ) xk ∼ G(α, βk, δ/k)
Proof: Since x ~ G(α, β, δ), for the second proposition
The proof of the first proposition is similar.
Property 2: If y = (x/β)δ and x ~ G(α, β, δ), then y has a gamma distribution x ~ G(α, 1, 1)
Proof: This follows from Property 1.
Thus, if F(x) is the cdf of G(α, β, δ) and H is the cdf of y = (x/β)δ, then F(x) = H(y). It also follows that
Property 3: If F(x) is the cdf of G(α, β, δ) and H is the cdf of y = (x/β)δ, then
F-1(p) = β ⋅ (H-1(p))1/δ
Related Distributions
Property 4: If x ~ G(1, β, δ) then x has a Weibull distribution (with alpha = β and beta = δ).
Proof: The pdf is
Property 5: If x ~ G(1, β, 1) then x has an exponential distribution (with lambda = 1/β).
Proof: This follows since an exponential distribution is equivalent to a gamma distribution with α = 1 and β = 1/λ.
It also follows from Property 4 since an exponential distribution is equivalent to a Weibull distribution (with alpha = β and beta = 1). Thus
Property 6: If x ~ G(1/2, β, 2) then x has a half-normal distribution
Here we are using the fact that Γ(1/2) = √π (see Gamma Function) Letting σ = β/√2, and so β = σ √π, we have
Moments
where
The following is a generalization of the formula for the mean:
Worksheet Functions
Real Statistics Functions: Starting with Rel 8.10, the Real Statistics Resource Pack will provide the following functions for the generalized gamma distribution:
GAMMA_DIST(x, α, β, δ, cum) = the pdf of the generalized gamma function f(x) when cum = FALSE and the corresponding cumulative distribution function F(x) when cum = TRUE.
GAMMA_INV(p, α, β, δ) = x such that GAMMA_DIST(x, α, β, δ, TRUE) = p. Thus, GAMMA_INV is the inverse of the CDF of the generalized gamma distribution.
Examples Workbook
Click here to download the Excel workbook with some examples that accompany this webpage.
References
Nematrian (2023) The generalised gamma distribution
http://www.nematrian.com/GeneralisedGammaDistribution
Jimenez Nava, V. H. (2011) Gamma and generalized gamma distributions
https://scholarworks.utep.edu/open_etd/2321/
Wikipedia (2023) Generalized gamma distribution
https://en.wikipedia.org/wiki/Generalized_gamma_distribution