Basic Concepts
The probability density function (pdf) and cumulative distribution function (cdf) of the Generalized Extreme Value (GEV) distribution are
where
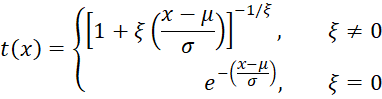
Note that when ξ ≠ 0
When ξ ≠ 0, then the domain of x is restricted to
Thus, these functions are defined for all x when ξ = 0, for all x ≥ μ – σ/ξ when ξ > 0, and for all x ≤ μ – σ/ξ when ξ < 0.
Outside this domain, we can consider f(x) = 0, and F(x) = 0 when ξ > 0 and F(x) = 1 when ξ < 0.
The inverse of the GEV distribution is
Relationship with Gumbel, Frechet, Weibull distributions
Fréchet: Let’s consider the standardized GEV distribution where μ = 0 and σ = 1, and let’s also assume that ξ > 0 and ξx > -1. Then the cdf can be expressed as
Now let y = ξx + 1, and so y > 0, and let β = 1/ξ. Then
which is the cdf at y = x/β + 1 of the (standardized) Fréchet’s distribution
Gumbel: The Gumbel distribution is the GEV distribution when ξ = 0.
Weibull: Let’s consider the standardized GEV distribution where μ = 0 and σ = 1, and let’s also assume that ξ < 0 and ξx > -1. Then the cdf is
Now let y = ξx + 1, and so y > 0, and let β = -1/ξ. Then
which is the cdf at y = 1 – x/β of the reverse Weibull distribution (with α = 1).
Properties
We now define
to obtain key statistical properties of the GEV distribution when ξ ≠ 0.
Figure 1 – Statistical properties of the GEV distribution
When ξ = 0, the GEV distribution is equivalent to the Gumbel distribution. See Gumbel Distribution for a description of the key properties in this case.
Worksheet Functions
Real Statistics Functions: The Real Statistics Resource Pack provides the following functions for the Gumbel distribution.
GEV_DIST(x, μ, σ, ξ, cum) = the pdf of the GEV distribution f(x) when cum = FALSE and the corresponding cumulative distribution function F (x) when cum = TRUE.
GEV_INV(p, μ, σ, ξ) = the inverse of the GEV distribution at p
Observation: If x has a GEV distribution, then x has a Gumbel, Fréchet or reverse Weibull distribution depending on whether ξ = 0, ξ > 0 or ξ < 0, respectively.
Extreme Value Applications and Theory
Click here for information about how the GEV distribution is used and also some additional properties about the distribution.
Click here for a description of the return period and return level and how to use the GEV distribution to address a practical problem.
References
NASA (2021) Generalized extreme value distribution and calculation of return value
https://gmao.gsfc.nasa.gov/research/subseasonal/atlas/GEV-RV-html/GEV-RV-description.html
MathWorks (2021) Generalized extreme value distribution
https://www.mathworks.com/help/stats/generalized-extreme-value-distribution.html
Wikipedia (2021) Generalized extreme value distribution
https://en.wikipedia.org/wiki/Generalized_extreme_value_distribution
Vose (2017) Generalized extreme value distribution
https://www.vosesoftware.com/riskwiki/Generalizedextremevaluedistribution.php
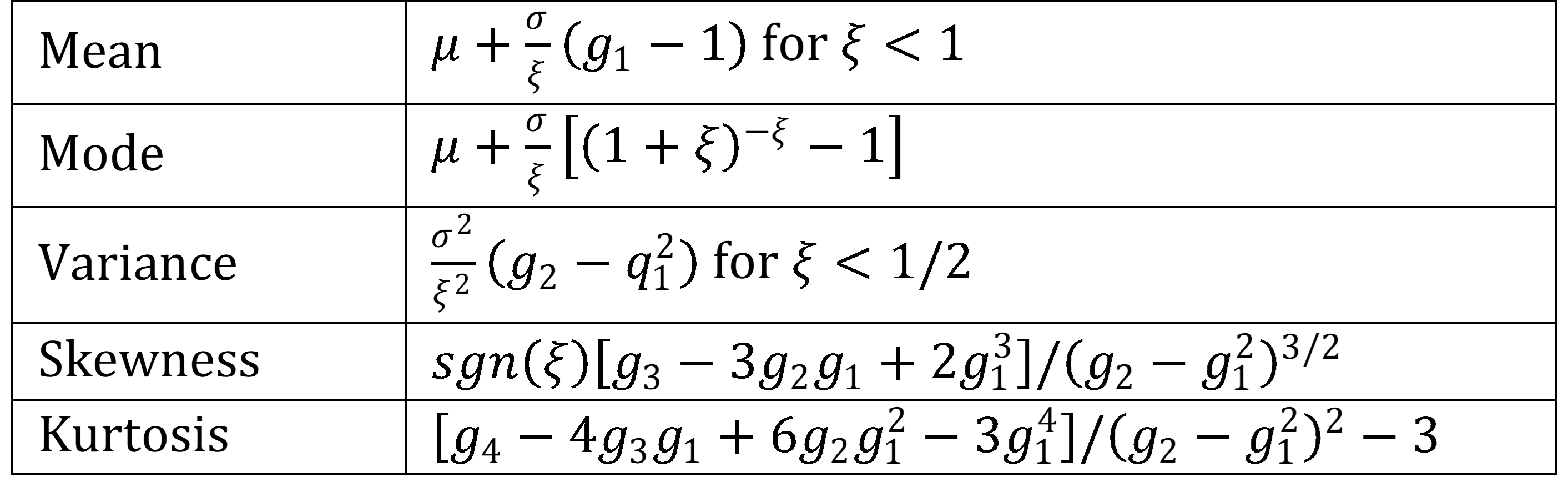
The spreadsheet sample Real-Statistics-Examples-Distributions.xlsx does not open properly (all the other examples spreadsheets open normally)
Hi Oene,
I just opened this workbook on my computer with no problems. What problem did you detect when you tried to open it?
Charles