Shape of the Gamma Function
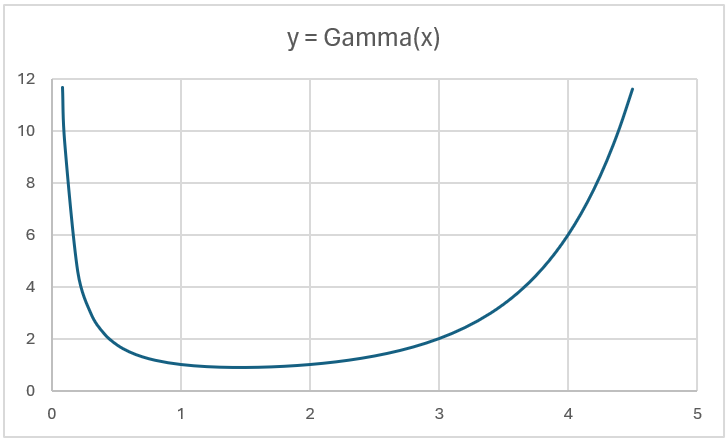
Figure 1 displays a graph of the gamma function y = Γ(x) between the values x = .82 and x = 4.5. The gamma function at either of these values is about 11.6, but clearly, the graph is not symmetric. Note that between 0 and 1, the graph grows very rapidly, and similarly for values larger than 4.5. In fact, as x → 0, y → ∞, and as x → ∞, y → ∞.
Finally, note that for any value of y, there are two positive values of x for which y = Γ(x). For example, Γ(4) = 6 and Γ(0.155222) = 6.
Figure 1 – Graph of the gamma function
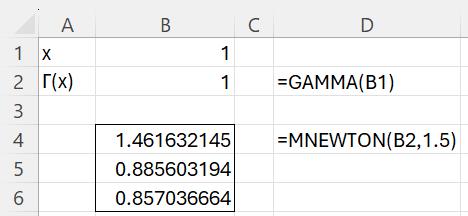
Note too that y = Γ(x) takes its minimum value at x = 1.461632, where Γ(x) = 0.885603. We can obtain this result by using Real Statistics’ MNEWTON function (see Minimum/Maximum Values of a Continuous Function) as shown in Figure 2.
Figure 2 – Minimum value of the gamma function
Here, we use x = 1.5 as our initial guess for the minimum value based on the graph in Figure 1 (actually, we could have even used an initial guess of 36 to obtain the same results). The values x = 1.461632, and Γ(x) = 0.885603 are shown in cells B4 and B5 of the output. That cell B6 contains a positive value indicates that we have found a local minimum.
Using Newton’s Method
Our goal is to calculate the inverse of the gamma function y = Γ-1(x). Thus, Γ-1(6) = 4 and 0.155222. Γ-1(0.885603), however, takes 1.461632 as its unique value. Values bigger than .885603 are on the upper branch of the graph, while values between 0 and .885603 are on the lower branch.
Note that in this analysis we will only consider positive real values.
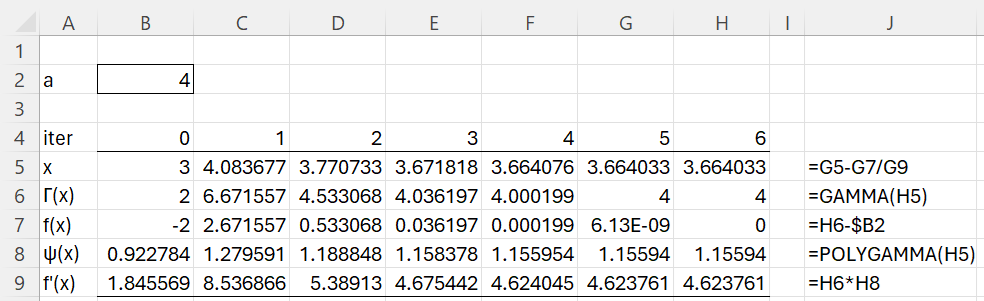
We now show how to find the inverse of the gamma function = Γ-1(a) for any value of a using Newton’s method. Figure 3 shows how to do this for a = 4. Finding the inverse gamma function value at 4 is equivalent to finding a root of the function f(x) = Γ(x) – 4.
Figure 3 – Calculating Γ-1(4) using Newton’s method
Column J contains the formulas used in column H. Similar formulas are used in columns B through G, except that B3 contains our initial guess of x = 3.
The approach illustrated uses the fact that the derivative of the gamma function Γ′(x) = Γ(x)ψ(x) where ψ(x) is the digamma function. We use Real Statistics’ POLYGAMMA(x) worksheet function to calculate the digamma function.
We see that after 5 iterations f(x) = 0 (cell G7) when x = 3.664033 (cell G5). Thus, the inverse of the gamma function at 4 is 3.664033. Actually, this is the solution for the upper branch of the gamma function.
Using the NEWTON worksheet function
We can also obtain the same result using Real Statistics’ NEWTON worksheet function, as shown in Figure 4. Note that in Figure 3 we used an initial guess of x = 3. Different initial guesses will result in different inverse function values, as shown in Figure 4.
Figure 4 – Calculating Γ-1(4) using NEWTON
The expression for our function is inserted in cell B3 (as shown in cell D3). We then insert an initial guess of 3 in cell G2 and other initial guesses in H2:T2. We next insert the formula =NEWTON($B3,G2) in cell G3 and =GAMMA(G3) in cell G4. Finally, we highlight the range G3:T4 and press the key sequence Ctrl-R to obtain the results shown in Figure 4.
When our initial guess is 3, we obtain the inverse of 3.664033, the same value obtained in Figure 3. The other initial guesses range from .01 to 37.2. When we use a small positive value as our initial guess, we obtain the left branch inverse gamma value of .227815. This is true for values up to about .44.
From about .45 to about 1.5, we then obtain a series of varying values, including negative inverse values of -1.24472, -1.85208, and -3.03973. Starting with initial guesses of about 1.6, we obtain the right branch inverse value of 3.664033. After about 37.2, we just get error values.
Conclusions
To obtain the left branch inverse value, we need to use an initial guess of a small positive value. The smaller the value of a in Γ-1(a), the smaller the initial guess must be. In fact, we can safely use min(a, ε) as our initial value where ε = some small value such as .000000001.
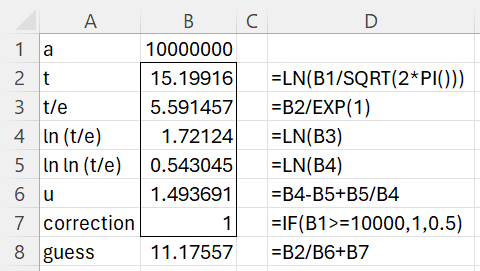
To obtain the right branch inverse value is more difficult since we need to choose an initial value in a specific range. For small values of a, up to about 2,000, guesses of 2, 3, 4, 5, 6, or 7 are adequate. It is not hard to determine a reasonable initial guess in each case. For larger values of a, we can calculate an initial guess as shown in Figure 5 for the case where a = 10,000,000.
Figure 5 – Calculating an initial guess for a > 2,000
The initial guess is a sufficiently good approximation of the real inverse, which is 11.42739.
Worksheet Function
To simplify our task, we can use the following worksheet function provided by the Real Statistics Resource Pack starting with Rel 8.10.
IGAMMA(x, upper, iter, prec) = the inverse gamma function value at x, where if upper = TRUE (default), then the larger inverse value is returned, while if upper = FALSE then the smaller value is returned.
iter (default 100) = the maximum number of iterations of Newton’s algorithm for finding the inverse, and prec is a small positive number (default 0.00000001) which determines when the algorithm terminates, indicating that no further improvement is necessary.
Note that the largest value of x supported by Excel is 1E+308 (actually 9.99999999999999E+307). The formula =IGAMMA(1E+308) returns the value 171.5103.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Wikipedia (2012) Gamma Function
https://en.wikipedia.org/wiki/Gamma_function
Wikipedia (2017) Digamma function
https://en.wikipedia.org/wiki/Digamma_function
Wikipedia (2012) Newton’s method
https://en.wikipedia.org/wiki/Newton%27s_method
Wiersma, A. (2016) The complex dynamics of Newton’s method
No longer available online