Gamma Function

Basic Concepts

The gamma function, denoted Γ(x), is commonly employed in a number of statistical distributions. Click here if you are interested in a formal definition that involves calculus, but for our purposes, this is not necessary. What is important are the following properties and the fact that Excel provides a function that computes the gamma function (as described below).

Property 1:

  1. Γ(1) = 1
  2. Γ(x + 1) = x Γ(x)
  3. Γ(n) = (n – 1)! for all non-negative integers n = 0, 1, 2, 3, …
  4. Γ(½) = \! \sqrt{\pi}

Based on Property 1, it follows that

Gamma multiples of .5

and so

Gamma multiples of .5

Graph of the Function

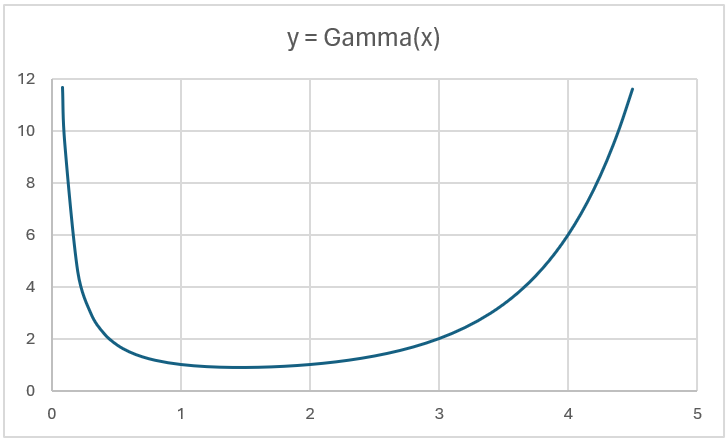
Figure 1 contains a graph of the function y = Γ(x) between the values x = .82 and x = 4.5. The gamma function at either one of these values is about 11.6, but clearly, the graph is not symmetric. Note that between 0 and 1 the graph grows very rapidly, and similarly for values larger than 4.5. In fact, as x → 0, y → ∞, and as x → ∞,  y → ∞.

Finally, note that for any value of y, there are two positive values of x for which y = Γ(x).

Gamma function graph

Figure 1 – Graph of the gamma function

Worksheet Function

Excel Function: Excel provides the following function:

GAMMALN(x) = ln Γ(x), i.e. the natural log of the gamma function.

Since the inverse of the log function is the exponential function (see Exponentials and Logs and Built-in Excel Functions), the gamma function can be expressed by the Excel formula:

Γ(x) = EXP(GAMMALN(x))

Alternatively, the gamma function can be calculated from Excel’s function for the gamma distribution (see Gamma Distribution) as follows:

Γ(x) = EXP(-1) / GAMMA.DIST(1, x, 1, FALSE)

For versions of Excel starting with Excel 2010, the function GAMMALN.PRECISE, is available which is equivalent to GAMMALN. Excel 2013 introduced the function GAMMA, where GAMMA(x) = Γ(x).

Inverse Gamma Function

Click here for information about the inverse gamma function.

Gamma function for negative values

The Excel functions described above only support positive values of x. Negative values can be defined via Property 1b, namely via Γ(x) = Γ(x+1)/x. Thus, by Property 1d, we see that Γ(-.5) = Γ(-.5+1)/(-.5) = -2\! \sqrt{\pi}.

Note that Γ(0) = Γ(1)/0, which is undefined. Thus, Γ(x) is undefined for x = 0, -1, -2, etc.

See Gamma Function Advanced for more details about the gamma function for negative values, including a Real Statistics worksheet function.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

Reference

Wikipedia (2012) Gamma Function
https://en.wikipedia.org/wiki/Gamma_function

24 thoughts on “Gamma Function”

  1. Hi Charles,
    Sorry i forgot to mention that i am trying to get the Weibull parameters. Those values in question are the X and Y from an axis graph.

    Many thanks in advance,

    Fernando

    Reply

  2. Hi Charles,
    Many thanks for replying my questions. Here i pose you the following example:
    cases Time between failures X= Ln(t-gamma) Y(ln(ln(1/(1-F(t-gamma)))))
    hrs
    1 0.167 -5.1589 -5.2958
    2 0.25 -2.4220 -3.9432
    3 0.33 -1.7617 -3.1833
    4 0.33 -1.7617 -3.1833

    This is for a Weibull application. I already calculated alpha, beta, r2, interception but i don´t know how to calculate the gamma function for all these data?. Have you got any idea?.

    Many thanks in advance.

    Fernando

    Reply

  3. Hi Charles,
    Yor explanations sounds very nice. I have one question; in case you have a column of various x values.How do you calculate the total GAMMA function

    Reply

    • Hello Fernando,
      You can calculate the value of the gamma function for each of the x values, but I don’t know what you mean by “the total GAMMA function”.
      Charles

      Reply

    • Yousef,
      Just use the formula =GAMMA(Pi()) to obtain 2.288037795 and =GAMMA(EXP(1)) to obtain 1.567468256.
      If your version of Excel doesn’t contain the function GAMMA(x), use the formula =GAMMALN(EXP(x)) instead.
      Charles

      Reply

    • Snil,
      In Excel, you can calculate the gamma function at x by =GAMMA(x) or by =EXP(GAMMALN(x)). Thus, the gamma function squared can be calculated by =GAMMA(x)^2 or by =EXP(GAMMALN(x))^2.
      Charles

      Reply

  7. Hello Charles! 😉 may i know what is/are the relation, uses and significance of the gamma function in some statistical distribution especially in Studentized range distribution? Thankyou for your response. 😉

    Reply

    • Myra,

      The gamma function is used in many distributions, including the t, chi and F distributions.

      Since n! is a special case of the gamma function, any distribution which uses the combination function C(n,p) is essentially using the gamma function. This includes the binomial distribution.

      The gamma function is also used to compute the Studentized range distribution.

      Charles

      Reply

      • Good day Sir. Sir i need to know what is the relation and connection of binomial distribution and studentized range distribution? Hoping for your response. More power! 😉

        Reply

  8. Charles,

    How can I calculate the Gamma function of a complex number in Excel 2010? Specifically, I want to calculate a Pearson Type IV distribution for which the normalizing constant involves GammaFunction(m + (nu/2) i), where m and nu are parameters.

    Tom

    Reply

  9. why do it appear as NUM! in my worksheet? please explain it
    i have equation “Gamma ((m/xi)+1)” but after I make a cell ((m/xi)+1), then use this function =EXP(GAMMALN(cell)) , then it appears as NUM!

    Reply

    • You may have an overflow error. Remember that Gamma(x) gets to be very large even for not so large values of x. In your case what is the value of x?
      Charles

      Reply

  10. Hello,

    Could you show me how to implement the Gamma Function as a Public User Defined Function in Excel 2010 using VBA Code. It should be very easy.

    Thank You
    Colm

    Reply

Leave a Comment