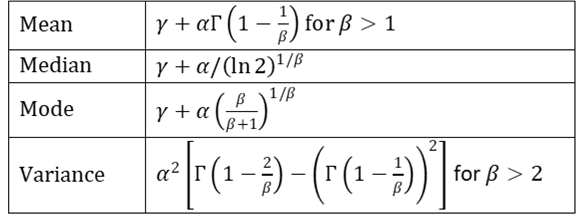Basic Concepts
The probability density function (pdf) of the Fréchet distribution is
for x ≥ γ. Here, γ is the location parameter, α > 0 is the shape parameter and β > 0 is the scale parameter.
The cumulative distribution function (cdf) is
The inverse cumulative distribution function is
Worksheet Functions
Real Statistics Functions: The Real Statistics Resource Pack provides the following functions for the Fréchet distribution.
FRECHET_DIST(x, α, β, γ, cum) = the pdf of the Fréchet distribution when cum = FALSE and the corresponding cumulative distribution function when cum = TRUE.
FRECHET_INV(p, α, β, γ) = the inverse of the Fréchet distribution at p
Properties
Key statistical properties of the Fréchet distribution are shown in Figure 1:
Figure 1 – Statistical properties of the Frechet distribution
Some additional properties:
If x ∼ Frechet(α, β, γ), then mx + c ∼ Frechet(mα, β, mγ+c) for constants m and c
If x ∼ Frechet(α, β, 0), then 1/x ∼ Weibull(1/α, β)
If x1, .., xn ∼ Frechet(α, β, γ), then the nth order statistic x(n) ∼ Frechet(αn1/β, β, γ)
Reference
Wikipedia (2021) Fréchet distribution
https://en.wikipedia.org/wiki/Fr%C3%A9chet_distribution