Interarrival Time
Example 1: On average, Florida experiences 5 lightning deaths per year. Assuming that lightning deaths are a random event, what is the probability that there will be no lightning deaths in the next 6 months?
Let x = the time to the first lightning death. Then x has an exponential distribution where λ = .5. Thus, we need to calculate
1 – EXPON.DIST(.5,5,TRUE) = 1 – .917915 = .082085 = 8.2%
Observation: We could use the exponential distribution to model the inter-arrival time between earthquakes or buses that arrive at random. If instead of lightning strikes we were trying to model the inter-arrival times of high tides or trains on a regularly scheduled route, we shouldn’t use the exponential distribution since these are not random events.
Mean Time to Failure
Example 2: The time until failure of a particular component in a mobile phone is known to follow an exponential distribution. If 10% of such components fail within 10,000 hours of use, what is the probability that one such component is still working after 40,000 hours of use? What is the mean time to failure (MTTF)?
Let x = the time to the first failure. Since has an exponential distribution, we can calculate the average number of failures per hour λ as follows:
.1 = P(x < 10000) = F(10000) = 1 – e–10000λ
Since .1 = 1 – e–10000λ, we have e–10000λ = .9, and so ln(e–10000λ) = ln(.9), from which it follows that -10000λ = ln(.9) = -.10536, and so λ = 1.5E-05.
Now, as we did in Example 1, the probability a component is still working after 40,000 hours is 65.6%, calculated as follows:
1 – EXPON.DIST(40000, 1.5E-05, TRUE) = .6561
From Figure 1, we see that the MTTF = 1/λ = 1/1.5E-.05 = 94,912 hours.
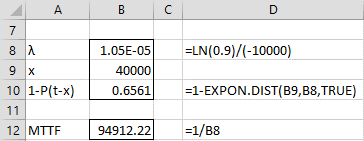
Figure 1 – MTTF using exponential distribution
Product Reliability Acceptance Testing
Suppose that you want to perform a product reliability acceptance test, whereby you guarantee that a product will meet some MTTF target based on an exponential distribution with 1 – α confidence. You can estimate the length of time you need to run the test by using the following Excel formula
=.5*MTTF*CHISQ.INV.RT(α, df)
where CHISQ.INV.RT is the inverse of the chi-square cdf (see Chi-square Distribution), df = 2(r+1), and r = the maximum number of failures that are acceptable in the test timeframe.
Product Reliability Acceptance Test Example
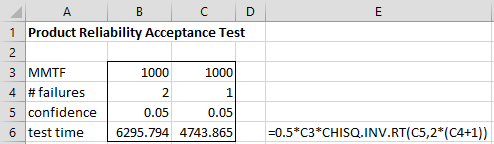
Example 3: A company is selling an electronic component and will pay heavy penalties if they don’t meet its claimed MTTF target of 1,000 hours. They have 5,000 hours of available test time and want to make sure that the component meets the MTTF by accepting 2 failures in the allotted time. For how many hours do they need to run the test?
As shown in column B of Figure 2, the company needs to run the test for at least 6,296 hours. If no more than 2 component failures are detected in this timeframe, then they can be 95% confident that the component will meet the MTTF target. Unfortunately, they don’t have 6,296 hours to test since any more than 5,000 hours will interfere with their normal production activities.
To reduce the time required for the test, they decide to accept at most one failure during the test. As can be seen from column C of Figure 2, only 4,744 hours of test time are required this time to make sure that the MTTF target is met with 95% confidence.
Figure 2 – Product Reliability Acceptance Testing
The longer test would have been preferable since there was less chance that the component would be rejected due to bad luck, but unfortunately, the longer test was not available. If two production lines were available then the longer test could have been performed in 6,296/2 = 3,148 hours using both production lines.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Reference
Wikipedia (2012) Exponential distribution
https://en.wikipedia.org/wiki/Exponential_distribution
NIST (2022) Exponential life distribution (or HPP model) tests
https://www.itl.nist.gov/div898/handbook/apr/section3/apr311.htm#:~:text=If%20it%20has%20no%20more,the%20equipment%20fails%20the%20test.