Exponential Distribution

Basic Concepts

The exponential distribution (aka the negative exponential distribution) can be used to determine the probability that it will take a given number of trials to arrive at the first success in a Poisson distribution; i.e. it describes the inter-arrival times in a Poisson process. It is the continuous counterpart to the geometric distribution, and it too is memoryless.

Definition 1: The exponential distribution has the probability density function (pdf) given by

f(x) = λe-λx

for x ≥ 0. Lambda is called the rate parameter and λ > 0.

The cumulative distribution function (cdf) is

F(x) = 1 – e-λx

The inverse cumulative distribution function is

F-1(p) = – ln(1–p)/λ

Worksheet Functions

Excel Function: Excel provides the following function for the exponential distribution:

EXPON.DIST(x, λ, cum) = the pdf of the exponential function f(x) when cum = FALSE and the corresponding cumulative distribution function F(x) when cum = TRUE.

This function is not available in versions of Excel before Excel 2010. Instead, these versions of Excel use the equivalent function EXPONDIST.

Observation: The exponential distribution is equivalent to the gamma distribution with α = 1 and β = 1/λ. Thus, EXPON.DIST(x, λ, cum) = GAMMA.DIST(x, 1, 1/λ, cum).

There is no EXPON.INV(p, λ) function in Excel, but GAMMA.INV(p, 1, 1/λ) or –LN(1–p)/λ or the following Real Statistics function can be used instead.

Real Statistics Function: The Real Statistics Resource Pack supplies the following function.

EXPON_INV(p, λ) = the inverse of the exponential distribution at p

Graph

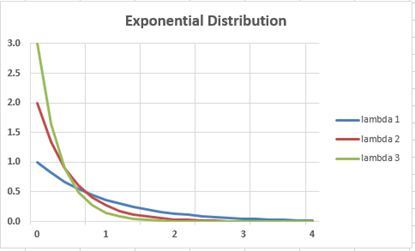
Figure 1 shows a graph of the pdf of the exponential distribution for λ = 1, 2, and 3.

Exponential distribution chart

Figure 1 – Pdf of exponential distribution

Properties

Key statistical properties are:

  • Mean = 1 / λ
  • Median = ln 2/λ
  • Mode = 0
  • Range = [0, ∞)
  • Variance = 1 / λ2
  • Skewness = 2
  • Kurtosis = 6

If λ is a constant representing the average number of random events that occur in a fixed time interval, then the probability that the first such event will occur in less than x time is given by the cumulative exponential distribution function F(x).

Property 1: An exponential distribution is memoryless

Property 2: If x has a Poisson distribution with mean λ, then the time between events follows an exponential distribution with mean 1/ λ.

Click here for the proofs of these two properties.

Related Distributions

  • If x ∼ Laplace(μ, β), then |x – μ| ∼ Exp(1/β)
  • If x ∼ Pareto(α, 1), then ln x ∼ Exp(α)
  • If x ∼ Exp(λ), then x ∼ Weibull(1/λ, 1)
  • If x ∼ Exp(λ), then x2 ∼ Weibull(1/λ2, 1/2)
  • If x ∼ Exp(λ), then e-x ∼ Beta(λ, 1)
  • If x ∼ Exp(λ), then kex ∼ Pareto(λ, k)

Examples

Click here for examples based on the exponential distribution.

Links

↑ Other key distributions

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

Reference

Wikipedia (2012) Exponential distribution
https://en.wikipedia.org/wiki/Exponential_distribution

18 thoughts on “Exponential Distribution”

  1. Hi Charles,

    This is a massive help. I think its exactly what I’ve been looking for.

    I want to conduct a simulation and I think part of it should be from the exponential dist.
    I’m simulating a utility over time. The utility value will be on the beta dist.
    The utility is inferred to be constant over time, so I plan to draw from the exponential dist on excel for the time period.

    I will use: LN(1 – RAND()) / -λ

    Do you think this approach sounds correct?
    Would you have any references for this?

    Many thanks
    B

    Reply

  2. Instead of using the Gamma.inv function, we can use the following formula:

    = LN(1 – RAND()) / -λ

    for simulation for an F(x) = RAND(), when we want to find the ‘x’.

    Reply

  6. Dear frinds
    Give me help
    I need a real data set in any field that have exponential distribution.
    size of data should be at least 300

    Reply

Leave a Comment