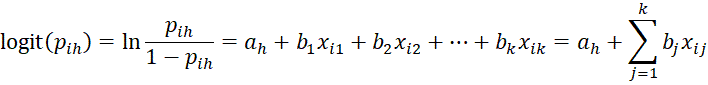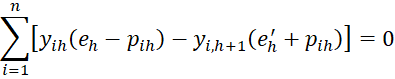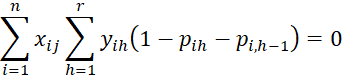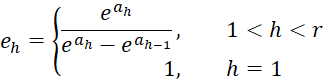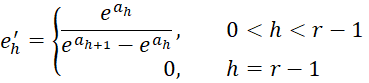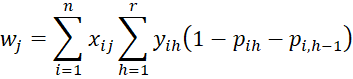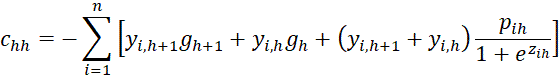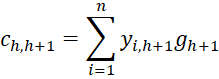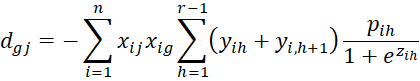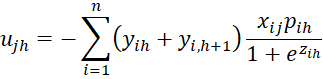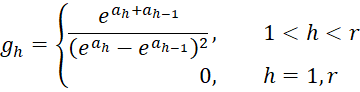Proportional Odds Model

Overview

We describe how to find the regression coefficients for the proportional odds model of ordinal regression (as described in Ordinal Regression Basic Concepts) using Newton’s method.

Suppose the possible outcomes for the dependent variable are 1, …, r. Let p_ih = P(y_i ≤ h), i.e. the cumulative probabilities. Thus 0 = p_i0 < p_i1 ⋯ < p_ir = 1  (thereby capturing the order of the outcomes), where p_i0 = 0 for notational convenience. Then for h = 1, …, r

P(y_i = h) = P(y_i ≤ h) – P(y_i ≤ h–1) = p_ih – p_ih-1

For the proportional odds model where the data {X₁, X₂, …, X_n} is a set of k-tuples X_i = (x_ij: j = 1 to k), we define the regression model

for each value of h = 1, …, r-1 and where for convenience we set x_i0 = 1. As explained in Ordinal Regression Basic Concepts, for each ordinal category h we use a separate intercept coefficient a_h but the same slope coefficients b_j. 

Note too that  a₁ < a₂ … < a_r-1. We also see that

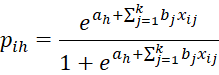
Log-Likelihood Function

Our goal is to find the values of the regression coefficients a₁,  … a_r-1, b₁, … b_k that maximize the log-likelihood function

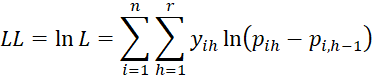
Property 1: The maximum value of the log-likelihood function LL occurs when the following r+k-1 equations hold for h = 1 to r-1.

or alternatively

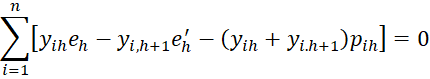and for j = 1 to k

where

Proof: click here

Newton’s Method

Property 2

Let

where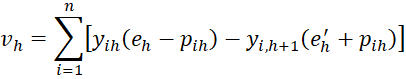

and J is the k+r-1 × k+r-1 symmetric matrix of form

where C = [c_hl] is an r-1 x r-1 matrix, D = [d_jg] is a k × k matrix and U = [u_jh] is an k × r-1 matrix consisting of the following elements

where

Then

B* = B – J^-1

is a better estimate of the coefficients than B (i.e. it produces a larger value for LL), and so the sequence B, B*, B**, B***, etc. converges to the coefficient vector that maximizes LL and the corresponding Hessian matrix J^-1 is a good estimate of the covariance matrix for the regression coefficients.

Proof: click here

Reference

Hyun Sun Kim (2004) Topics in ordinal logistic regression and its applications. Dissertation Texas A & M
http://oaktrust.library.tamu.edu/handle/1969.1/1120